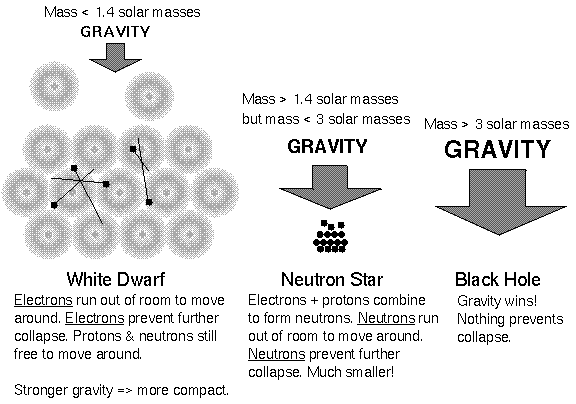
If the core mass is between 1.4 and 3 solar masses, the compression from the star's gravity will be so great the protons fuse with the electrons to form neutrons. The core becomes a super-dense ball of neutrons. Only the rare, massive stars (about 8 to 25 solar masses) will form these remnants in a supernova explosion. Neutrons can be packed much closer together than electrons so even though a neutron star is more massive than a white dwarf, it is only about the size of a city.

The neutrons are degenerate and their pressure (called neutron degeneracy pressure) prevents further collapse. Neutron stars are about 30 kilometers across, so their densities are much larger than even the incredible densities of white dwarfs: 200 trillion times the density of water (one sugar cube volume's worth has a mass = mass of humanity)! The superior resolution of the Hubble Space Telescope has enabled us to directly image a few of these very small objects in visible light. The first image in visible light of a lone neutron star is shown in the figure below (the arrow points to it). Even though it is over 660,000 K, the neutron star is close to the limit of HST's detectors because it is at most 27 kilometers across. This one is at most 400 light years away. The closest known neutron star is about 200 light years away.

Normal variable stars (stars near the end of their life in stages 5 to 7) oscillate brightness by changing their size and temperature. The density of the star determines the pulsation period---denser stars pulsate more quickly than low density variables. However, normal stars and white dwarfs are not dense enough to pulsate at rates of under one second. Neutron stars would pulsate too quickly because of their huge density, so pulsars must pulsate by a different way than normal variable stars. A rapidly rotating object with a bright spot on it could produce the quick flashes if the bright spot was lined up with the Earth. Normal stars and white dwarfs cannot rotate fast enough because they do not have enough gravity to keep themselves together; they would spin themselves apart. Neutron stars are compact enough and strong enough to rotate that fast. The pulsar at the center of the Crab Nebula rotates 30 times every second. In the figure below, it is the left one of the two bright stars at the center of the Hubble Space Telescope image (right frame).

Another clue comes from the length of each pulse itself. Each pulse lasts about 1/1000th of a second (the time between pulses is the period mentioned above). An important principle in science is that an object cannot change its brightness faster than it takes light to cross its diameter. Even if the object could magically brighten everywhere simultaneously, it would take light from the far side of the object longer to reach you than the near side. The observed change in brightness would be smeared out over a time interval equal to the time it would take the light from the far side of the object to travel to the near side of the object. If the object did not brighten everywhere simultaneously, then a smaller object could produce a pulse in the same interval. The brightness fluctuation timescale gives the maximum size of an object. Since the diameter = (fluctuation time) × speed, the maximum possible diameter = (fluctuation time) × (speed of light).
|
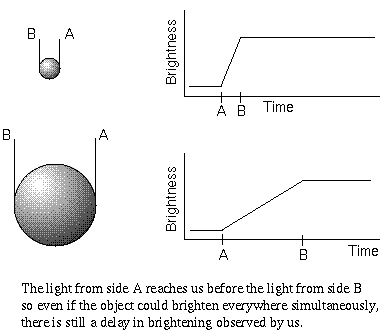 |
The 1/1000th of second burst of energy means that the pulsars are at most (300,000 kilometers/second) × (1/1000 second) = 300 kilometers across. This is too small for normal stars or white dwarfs, but fine for neutron stars (they are actually less than 30 kilometers across). When neutron stars form, they will be spinning rapidly and have very STRONG magnetic fields (109 to 1012 times the Sun's). The magnetic field is the relic magnetic field from the star's previous life stages. The magnetic field is frozen into the star, so when the core collapses, the magnetic field is compressed too. The magnetic field becomes very concentrated and much stronger than before.
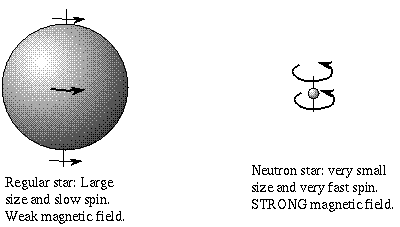
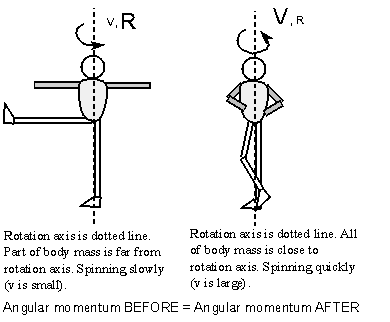
Why would neutron stars be fast rotators? Conservation of angular momentum! Just as a spinning ice skater can spin very fast by pulling in her arms and legs tight about the center of her body, a star will spin faster when it brings its material closer to its center. The angular momentum of an object = its mass × its equatorial spin speed × its radius. The mass remains constant. In order to keep the angular momentum constant the spin speed must increase if the radius decreases. This will keep the product of spin speed × radius the same value. A slowly rotating red giant star will have the same angular momentum when it becomes a tiny, fast rotating neutron star. See the Angular Momentum appendix for other examples.
The neutron star's magnetic field lines converge at the magnetic poles, so the charges get focused and a narrow cone of non-thermal radiation is beamed outward. If the beam sweeps past Earth, you see a flash of light. However, given the wide range of angles the magnetic poles could be aligned in space, it is more likely that the beam will miss the Earth. There are probably many more pulsars out there that cannot be detected because their beams do not happen to cross our line of sight.
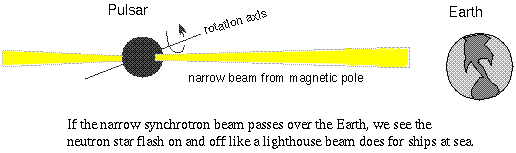
The energy of the non-thermal radiation beam comes from the rotational energy of the pulsar. Since the light energy escapes, the production of the energy beam robs energy from the pulsar, so the pulsar's rotation slows down (angular momentum does slowly decrease). Another equivalent way to view the process is from Newton's 3rd law of motion. The magnetic field exerts a force on the charged particles, speeding them up. The charged particles exert a reaction force on the magnetic field slowing it and the pulsar down. Eventually, the pulsar dies away when the neutron star is rotating too slowly (periods over several seconds long) to produce the beams of radiation.
Every now and then, a ``glitch'' is seen in the pulse rate of a pulsar. The pulsar suddenly increases its spin rate. What causes this is the neutron star suddenly shrinks by about 1 millimeter. The spin rate suddenly increases to conserve angular momentum. The spin rate can be greatly increased if the pulsar is in a close binary system and its companion dumps gas onto the pulsar. The pulsar gains angular momentum from the incoming gas and ramps up its spin rate as more gas falls onto it. The pulsars that spin hundreds of times per second are thought to be the result of such a transfer.
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: April 9, 2024