This material (including images) is copyrighted!. See my copyright notice for fair use practices.
Just like you found for the determination of stellar properties, finding the distance to the galaxies is essential for comparing the galaxies against each other. In order to determine the luminosities and masses of the galaxies and the distribution of the mass inside the galaxies, you must first know the distances to them. Is that galaxy in our telescope bright because it is producing a lot of energy or because it is close to us? Are the stars moving quickly in a galaxy because the combined mass is large or because the distances inside the galaxy are small? You need to find the distance to the galaxy to be sure.
One method of determining the distance discussed above uses the period-luminosity relation of Cepheid variable stars to derive the distance from the apparent brightness of the Cepheids. This works for the nearby galaxies. To find the distance to galaxies farther away, other standard candle techniques involving objects more luminous than Cepheids like Type Ia supernova explosions or supergiant stars are used. Supergiant luminosities are not as well known or uniform as the Type Ia supernovae, so astronomers prefer to use the Type Ia supernovae to derive the distances to the very distant galaxies.
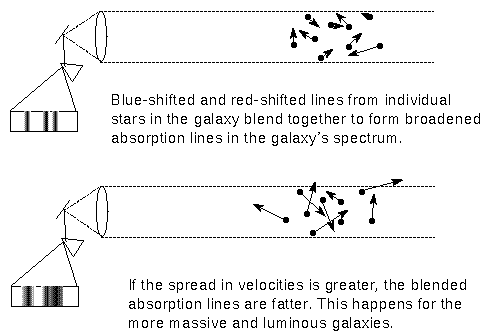
Another method uses the width of a galaxy's spectral lines. The width of the absorption lines from the stars or the radio emission lines from the gas in a galaxy depend on the amount of stellar motion in the galaxy. Most galaxies are too far away for us to resolve the fine-scale details of the internal motions in the galaxies. The spectrum of far away galaxies is from the combined motions of all of the material in them.

Some stars in a far away galaxy are moving toward us, so their absorption lines will be blueshifted. Other stars will have redshifted lines because they are moving away from us. The resulting spectral lines from the entire galaxy blend together to form a FAT line. The same effect is seen with the gas motions (caused by heat and rotation) inside a single star or gas cloud in our galaxy. The more random motion there is in an elliptical galaxy, the greater the spread in the distribution of velocities and the fatter the resulting galaxy spectral lines will be. More massive galaxies have more gravity so their stars are accelerated to faster orbital speeds. More massive galaxies should have broader lines and if the luminosity correlates with the mass, the more massive galaxies should have greater luminosity.
Sandra Faber and Robert Jackson discovered in 1976 a simple relation between the spread of velocities (called the velocity dispersion) and the luminosity of elliptical galaxies. For the inner few kiloparsecs of the elliptical galaxies, the velocity dispersion = 220 × (L/L*)0.25, where L* is a characteristic galaxy luminosity (around 10 billion solar luminosities). This is known as the Faber-Jackson relation. An elliptical galaxy's luminosity can be found from the velocity dispersion of the stars in the central few kiloparsecs of the galaxy.
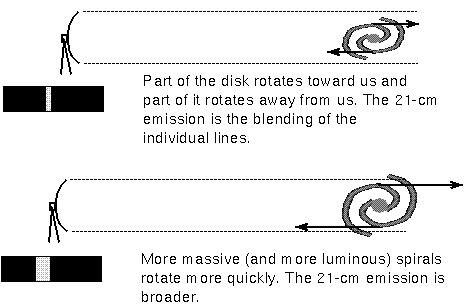
In 1977 Brent Tully and Richard Fisher discovered a similar relation between the rotational velocity of the disk and the luminosity of a spiral galaxy. The rotational velocity is found from the 21-cm emission of the neutral atomic hydrogen gas in the outer parts of the disk. The rotation curve is flat in the outer parts of most galactic disks (dark matter!). The part of a spiral galaxy's disk that is rotating toward us will have its lines blueshifted. The part of the disk rotating away from us will have its lines redshifted. The 21-cm emission from a galaxy of small angular size will be the blended result of the emission from all parts of the disk. The faster the disk rotates, the broader the 21-cm emission line will be. The Tully-Fisher relation for the infrared luminosity is: circular velocity = 220 × (L/L*)0.22. Infrared is used to lessen the effect of the dust in our galaxy and in the other spiral galaxy. The luminosity of the galaxy is found from the width of the 21-cm emission line and the distance is then derived using the apparent brightness and the inverse square law. The methods of determining the distances to the galaxies are summarized in the ``Steps to the Hubble Constant'' section.
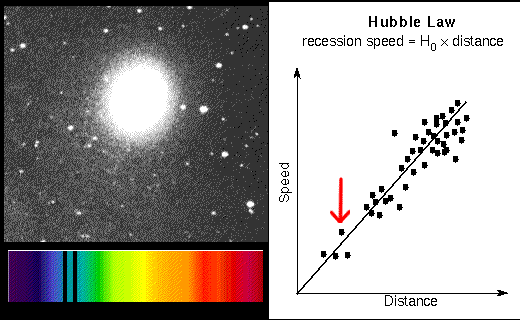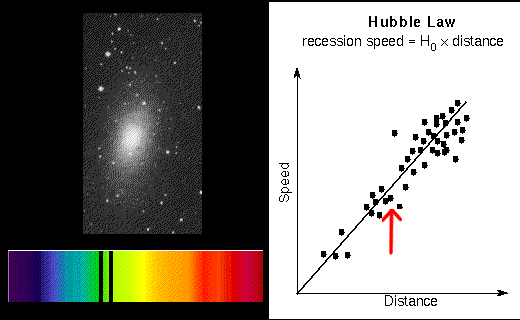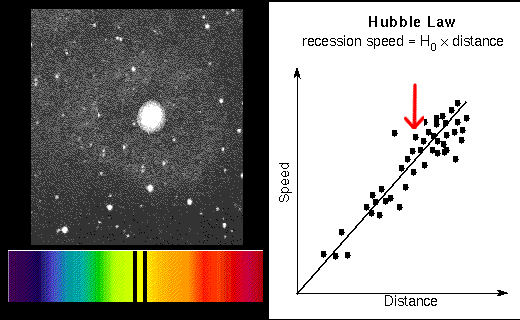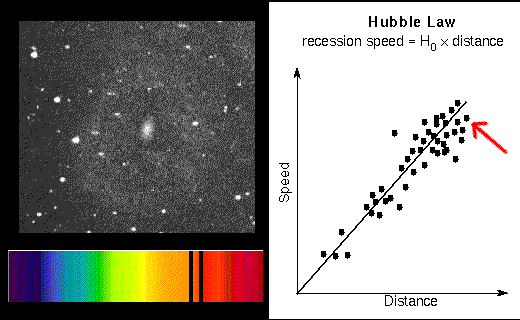
If the distance is measured in units of megaparsecs (Mpc) and the recession speed is in kilometers/second (km/sec), the Hubble constant (slope of the line) is between 70 and 80 km/sec/Mpc. This value is found by using the galaxies that have accurate distances measured (Cepheids, etc.) and dividing their recession speeds by their distances. It is easy to find the recession speeds of galaxies from their redshifts. The Hubble-Lemaître law provides an easy way to measure the distances to even the farthest galaxies from the (recession speed/H). For example, if a galaxy has a redshift of 20,000 km/sec and H is set to 70 km/sec/Mpc, then the galaxy's distance = (20,000 km/sec)/(70 km/sec/Mpc) = 20,000/70 × [(km/sec)/(km/sec)] Mpc = 286 megaparsecs.
At first glance it looks like the Milky Way is at the center of the universe and it committed some galactic social blunder because all of the other galaxies are rushing away from it (there are a few true galactic friends like the Andromeda Galaxy that are approaching it). The Hubble-Lemaître Law shows that there is actually not a violation of the Copernican principle. Because the more distant galaxies move faster, this means that the galaxies (or galaxy clusters) are all moving away from each other---the universe is expanding uniformly. Every other galaxy or galaxy cluster is moving away from everyone else. Every galaxy would see the same Hubble-Lemaître Law.
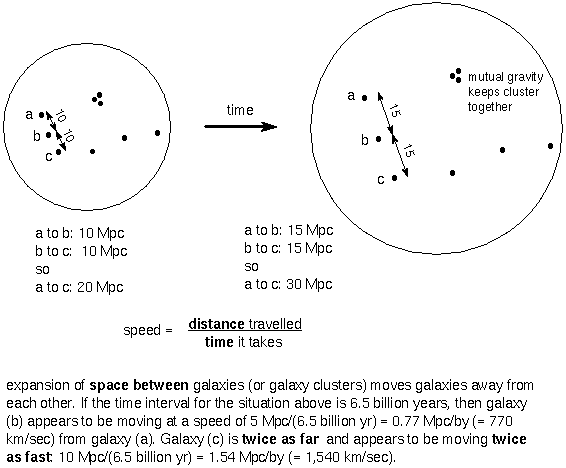
In the next chapter you will see that the expansion of the universe is the expansion of space itself---the galaxies are not moving through space, but, rather, they are being carried along with the expansion of space. For now, use the figure above to see how a uniform expansion gives us the Hubble-Lemaître Law. Since space itself expands, all distances will increase by the same factor in the same amount of time. Galaxy (a) is 10 megaparsecs from galaxy (b) and galaxy (c) is 10 megaparsecs from galaxy (b). If the Hubble constant this time is 77 km/sec/Mpc, then galaxy (a) sees galaxy (b) moving at 770 kilometers/second away from it and galaxy (c) is moving away from galaxy (b) at 770 kilometers/second. Astronomers on galaxy (a) will see the galaxy (c) moving away at (770 + 770) kilometers/second = 1,540 kilometers/second, twice as fast as galaxy (b), because galaxy (c) is at a distance of (10 + 10) megaparsecs from galaxy (a), twice as far as galaxy (b).
The galaxy (a) astronomers see the other galaxies moving away from them and their home galaxy appears to be at rest. Now jump to galaxy (c). To the astronomers on galaxy (c), galaxy (a) is moving away at 1,540 kilometers/second and galaxy (b) is moving away at 770 kilometers/second. Their home galaxy (c) appears to be at rest. You can use similar reasoning to show that everybody will also get the same numerical value for the Hubble constant. The figure above also illustrates another point about the expansion. Notice that the sizes of the dots and the size of the threesome group at center-top do not change. The galaxies themselves do not expand and the galaxies inside a cluster do not expand away from each other. On small size scales, the internal gravity of a galaxy or galaxy cluster prevents the expansion inside the galaxy or galaxy cluster. The Hubble-Lemaître Law applies for only the very large distances.
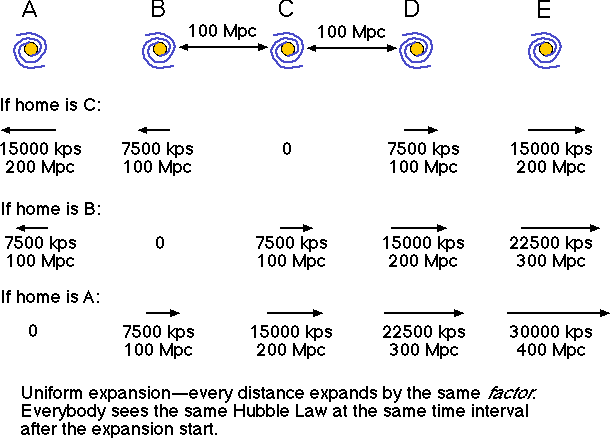
Another example of how everyone will see the same Hubble-Lemaître Law is given in the figure below. Each of the galaxies in the figure is 100 million parsecs (about 300 million light years) apart from each other and the Hubble constant is set to 75 km/sec/Mpc here. If you choose galaxy C to be your home galaxy, then you will see galaxies B and D moving at 7,500 kilometers/second away from you because they are at a distance of 100 megaparsecs from you. Galaxies A and E are 100 megaparsecs from their closest neighbors, so they are moving away from them at 7,500 kilometers/second and 15,000 kilometers/second away from galaxy C since they are each 200 megaparsecs from galaxy C. What would the galaxy speeds be if you chose galaxy D or galaxy E as your home galaxy?
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 28, 2022