Universal Law of Gravity

Chapter index in this window —   — Chapter index in separate window

Video lecture for this chapter

This material (including images) is copyrighted!. See my copyright notice for fair use practices. Select the photographs to display the original source in another window.

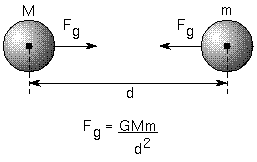
Using Kepler's third law and his own second law, Newton found that the amount of the attractive force, called gravity, between a planet and Sun a distance d apart is Force = kp × (planet mass) / (d)2, where kp is a number that is the same for all the planets. In the same way he found that the amount of the gravity between the Sun and a planet is Force = ks × (Sun mass) / (d)2. Using his third law of motion, Newton reasoned that these forces must be the same (but acting in the opposite directions). He derived his Law of Gravity: the force of gravity = G × (mass #1) × (mass #2) / (distance between them)2 and this force is directed toward each object, so it is always attractive. The term G is a universal constant of nature. If you use the units of kilograms (kg) for mass and meters (m) for distance, G = 6.672 × 10-11 m3 /(kg sec2). If you need a refresher on exponents, square & cube roots, and scientific notation, then please study the math review appendix.

Spherically symmetric objects (eg., planets, stars, moons, etc.) behave as if all of their mass is concentrated at their centers. So when you use Newton's Law of Gravity, you measure the distance between the centers of the objects.

Law of Gravity

In a bold, revolutionary step, Newton stated that his gravity law worked for any two objects with mass---it applies for any motions on the Earth, as well as, any motions in space. He unified celestial and terrestrial physics and completed the process started by Copernicus of removing the Earth from a unique position or situation in the universe. His law of gravity also explained Kepler's 1st and 2nd laws.

The UNL Astronomy Education program's Planetary Orbit Simulator shows you how a planet's velocity and accelearation relate to its orbits and Kepler's laws (link will appear in a new window).

Characteristics of Gravity

Newton's Law of Gravity says a lot about this force in a very compact, elegant way. It says that any piece of matter will feel it whether it is charged or not (this sets it apart from electrical and magnetic forces that affect only charged objects). Gravity depends only on the masses of the two attracting objects and their distance from each other. It does not depend on their chemical composition or density. A glob of peanut butter the mass of the Sun will have the same gravitational effect on the Earth as the Sun does. Gravity is always attractive, never repulsive (this is another way it is different from electrical and magnetic forces).

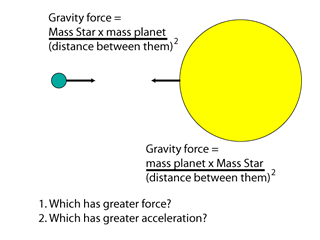
Because the masses are in the top of the fraction, more mass creates more gravity force. This also means that more massive objects produce greater accelerations than less massive objects. Since distance is in the bottom of the fraction, gravity has an inverse relation with distance: as distance increases, gravity decreases. However, gravity never goes to zero---it has an infinite range (in this respect it is like the electrical and magnetic forces). Stars feel the gravity from other stars, galaxies feel gravity from other galaxies, galaxy clusters feel gravity from other galaxies, etc. The always attractive gravity can act over the largest distances in the universe.

There is no way to get rid of the force of gravity. If you want to prevent a body from producing a gravitational acceleration on an object, you need to use a second body, with the same amount of gravity pull as the first body, in a way that its gravity pulling on the object is in the opposite direction. The resulting accelerations due to the forces from the two bodies will cancel each other out.

Review Questions

  1. What basic fundamental assumption did Newton make about the laws of nature on the Earth and in space?
  2. Why is gravity often the most important force in astronomical interactions?
  3. What things does gravity depend on?
  4. How does gravity vary with distance between objects and with respect to what do you measure the distances?
  5. What would happen to the orbit of Io (one of Jupiter's moons) if all of the Hydrogen and Helium in Jupiter were converted to Silicon and Oxygen? Explain your answer.
  6. What would happen to the Earth's orbit if the Sun suddenly turned into a black hole (of the same mass)? Why?
  7. How would antimatter respond to gravity? (Hint: antimatter has mass just like ordinary matter.)
  8. What important laws of planet motion can be derived from Newton's law of gravity?
  9. Use Newton's laws of motion and gravity to answer the two questions given in the figure below.
    star pulling on planet, planet pulling on star

previousGo back to previous section -- next Go to next section

Go to Astronomy Notes home

last updated: February 21, 2022

Is this page a copy of Strobel's Astronomy Notes?
Author of original content: Nick Strobel