This material (including images) is copyrighted!. See my copyright notice for fair use practices.
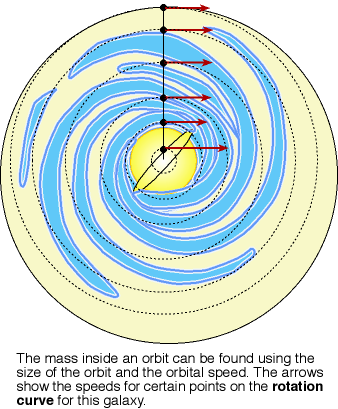
Recall from the Gravity Applications chapter that if you know the size of an object's orbit and how quickly it is moving in its orbit, you can find the mass of the central object, or the mass of the two object's orbiting around a common point. The same principle can be used to calculate the mass of the Galaxy! (Isn't gravity wonderful?) In this case, the two masses involved are the mass of the star and the mass of the part of the Galaxy that is inside the star's orbit. For most orbits the Galaxy mass inside the orbit is MUCH larger than the star's mass, so it is safe to ignore the star's mass.

The gravity from the part of the Galaxy inside the star's orbit accelerates the star so it moves in an orbit. The greater the gravity pulling on a star, the faster the star will move. Applying the mass and orbit speed relations of the gravity chapter, the enclosed mass inside the star's orbit = (orbital speed)2 × (star's distance to the galactic center)/G, where G is the gravity constant. The Galaxy's mass is found from measuring the orbital speed of stars (or gas clouds) and their distance from the center.
From measurements of stars and hydrogen clouds in the galactic disk, astronomers construct a rotation curve for the Galaxy. This is a plot of the orbital speed of stars (or gas clouds) vs. their distance from the center of the Galaxy. The "rotation" part of the term refers to the motion of the disk as a whole. As a whole the disk seems to be rotating (spinning) even though it is really the individual stars and clouds that are orbiting around the center. The rotation curve tells you the amount of mass inside a given distance from the center. You find how the mass is distributed in the Galaxy by looking at how the amount of enclosed mass changes with the size of the orbits.
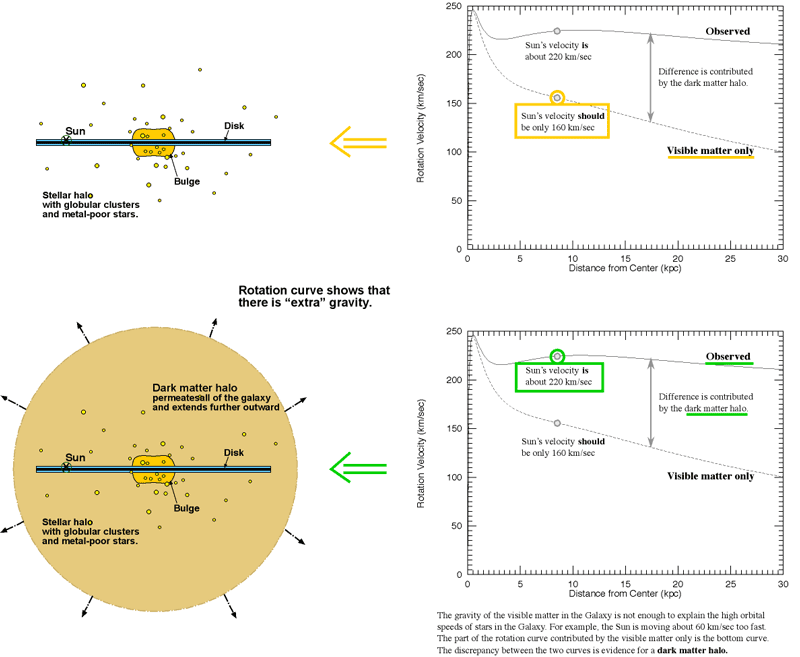
A rigid body rotation is seen close to the center (as if the part close to the center was rotating as one single object even though it is made of stars and gas), then the curve drops off, then rises, and eventually flattens out as far out as can be seen. Because gravity becomes weaker with larger (increasing) distance, the stars on the outskirts of the visible galaxy should be moving slower than those closer to where most of the visible mass resides. Instead, they are moving at about the same speed, even though they are farther from most of the visible matter! There must be extra mass in the Galaxy we cannot see to create the extra amount of gravity force. The Galaxy is spinning too quickly---the visible matter does not have enough mass to keep the Galaxy together! [Recent measurements on the size of the Milky Way using the VLBA have scaled the distances and speeds up---the Sun's distance from the center is 8.15 kpc and the circular rotation speed at the Sun's position is 236 km/sec---but how the speeds change with distance, the shape of the rotation curve, is still as described here.]
The observed rotation curve can be decomposed into the individual parts contributed by each component of the Galaxy: the disk, bulge + stellar halo, and the rest of total mass is what is called dark matter---material that does not emit any light (a small fraction of it is ordinary matter that is too faint to be detected yet) but has a significant amount of gravitational influence. The highest solid line in the left plot below is for all of the galactic components combined. The other curves (dashed, dotted, and solid) are the contributions of the individual galactic components (the bulge + stellar halo = "bulge", disk, and the dark matter halo) to the rotational velocity. In the figure below, the dark matter halo is called the "corona". Select the image to show a magnified view in another window. (The particular model used for these curves is what I used for my dissertation research in 1994-1995.)
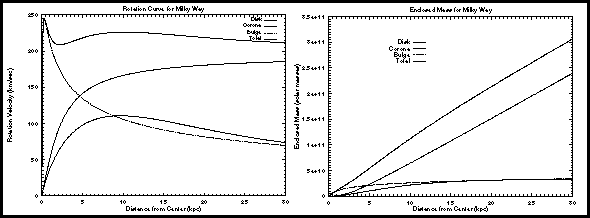
The plot on the right shows the enclosed mass inside a given distance. If you reach the point where the enclosed mass does NOT increase with distance, then you will have found the edge of the Galaxy's mass. Beyond the edge of the Galaxy, the rotational velocity will decrease as the distance from the center increases. Both plots show that the end of the Galaxy's mass has not yet been found but measurements of very distant globular clusters by Gaia and the Hubble Space Telescope in 2019 seem to indicate a total galactic mass of 1.5 trillion solar masses within a distance of 129,000 light years from the galactic center. The stars, dust, and gas in the disk and stellar halo do not explain all the mass. The part of the Galaxy that fills up the remainder of mass is the dark matter halo (corona). Ninety percent of the Galaxy's mass is in the form of this dark matter! Unfortunately, because gravity depends only on the distance and mass and not the composition, astronomers are not certain what the dark matter is composed of. It could be in the form of planets, brown dwarfs (stars too small to shine from nuclear fusion), white dwarfs, black holes, neutrinos with mass, or other exotic particles that have not been discovered in the laboratory yet. For reasons to be explained in the galaxy chapter and cosmology chapter, astronomers have figured out that the dark matter is a combination of all those things but the exotic particles must make up the vast majority of the dark matter. In fact, of the total matter in the universe, the overall mass of the exotic particles is five times the overall mass of the "ordinary matter" we are more familiar with (matter made of protons, neutrons, electrons, neutrinos, etc.).
You may be a bit skeptical about the existence of this dark matter. Are not astronomers going "too far" with their speculations? Scientists, by nature, are skeptical themselves of any radical change in our understanding of the universe. However, nature and careful observations are the sole judge of scientific truth and even the smartest scientist must yield to what nature is telling us. The conclusion that dark matter exists has come from using the standard scientific method of observation, interpretation, and testing of the explanation. Looking back in history, the detection of dark matter is just another application of Newton's law of gravity. Until Neptune was directly observed, its presence was known from its gravitational effect on Uranus (Neptune was "dark matter"). Astronomers have used the orbits and wobbling of stars to detect the presence of as yet, unseen companions around them (i.e., exoplanets and black holes). The exoplanets and black holes are technically, dark matter too. They may be faint or invisible themselves, but they produce definite gravitational effects on nearby visible objects. At the other end of the scale, no one has ever directly seen an electron, but you know such a particle exists and it is essential to our society of electricity and electronics.
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 27, 2022