Video lecture for this chapter
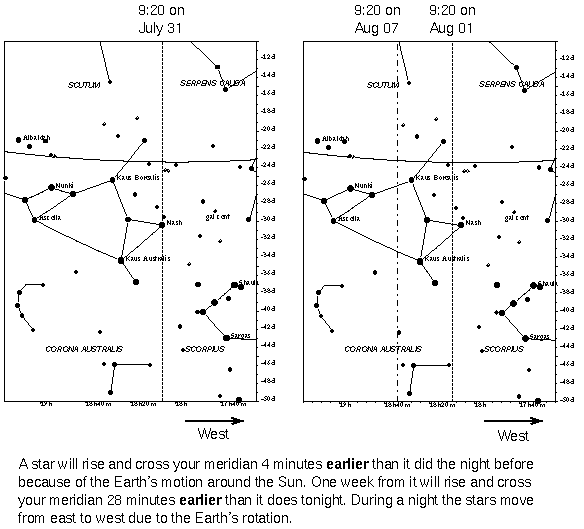
The fact that our clocks are based on the solar day and the Sun appears to drift eastward with respect to the stars (or lag behind the stars) by about 1 degree per day means that if you look closely at the positions of the stars over a period of several days, you will notice that according to our clocks, the stars rise and set 4 minutes earlier each day. Our clocks say that the day is 24 hours long, so the stars move around the Earth in 23 hours 56 minutes. This time period is called the sidereal day because it is measured with respect to the stars. This is the true rotation rate of the Earth and stays the same no matter where the Earth is in its orbit---the sidereal day = 23 hours 56 minutes on every day of the year. One month later (30 days) a given star will rise 2 hours earlier than it did before (30 days × 4 minutes/day = 120 minutes). A year later that star will rise at the same time as it did today.

Another way to look at it is that the Sun has made one full circuit of 360 degrees along the ecliptic in a year of 365.24 days (very close to 1 degree per day). The result is that between two consecutive meridian crossings of the Sun, the Earth has to turn nearly 361 degrees, not 360 degrees, in 24 hours. This makes the length of time for one solar day to be a little more than the true rotation rate of 23 hours 56 minutes with respect to the background stars.
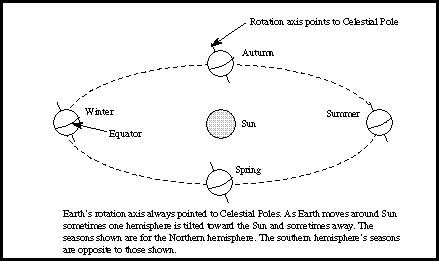
Note that the Earth's rotation axis is always pointed toward the Celestial Poles. Currently the North Celestial Pole is very close to the star Polaris. The figure above shows this view of the Earth's nearly circular orbit from slightly above the orbital plane (hence, the very elliptical appearance of the orbit).
Imagine that at noon there is a huge arrow that is pointing at the Sun and a star directly in line behind the Sun. The observer on the Earth sees the Sun at its highest point above the horizon: on the arc going through the north-zenith-south points, which is called the meridian. The observer is also experiencing local noon. If the Sun were not there, the observer would also see the star on the meridian.
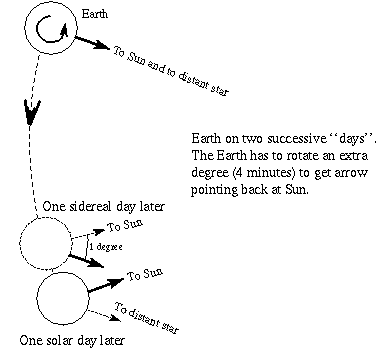
Now as time goes on, the Earth moves in its orbit and it rotates from west to east (both motions are counterclockwise if viewed from above the north pole). One sidereal period later (23 hours 56 minutes) or one true rotation period later, the arrow is again pointing toward the star. The observer on the Earth sees the star on the meridian. But the arrow is not pointing at the Sun! In fact the Earth needs to rotate a little more to get the arrow lined up with the Sun. The observer on the Earth sees the Sun a little bit east of the meridian. Four minutes later or one degree of further rotation aligns the arrow and Sun and you have one solar day (24 hours) since the last time the Sun was on the meridian. The geometry of the situation also shows that the Earth moves about 1 degree in its orbit during one sidereal day. That night the Earth observer will see certain stars visible like those in Taurus, for example. (Notice that the Earth's rotation axis is still pointed toward Polaris.) A half of a year later Taurus will not be visible but those stars in Scorpius will be visible. (Again, notice that the Earth's rotation axis is still pointed toward Polaris.) The extra angle any planet must rotate on its axis to get the Sun back to the meridian equals the angle amount the planet moved in its orbit in one sidereal day.
The amount of time it takes to spin the extra angle = (extra angle amount)/(spin rate). For the Earth, the spin rate = 360°/23.9333 hours = 15°/hour or 1°/4 minutes. Notice that I converted 23 hours 56 minutes to a decimal fraction of hours before I did the division. The amount of time between the solar day and sidereal day = (1 degree)/(1 degree/4 minutes) = 4 minutes.
The Earth's sidereal day is always 23 hours 56 minutes long because the number of degrees the Earth spins through in a given amount of time stays constant. If you are a careful observer, you will notice that the solar day is sometimes slightly longer than 24 hours and sometimes slightly shorter than 24 hours during the year. The reason for this is that the Earth's orbit around the Sun is elliptical and that the Sun's motion is not parallel to the celestial equator. The effects of this are explained fully in the Equation of Time section below. The value of 24 hours for the solar day is an average for the year and is what our time-keeping system is based on.
The precession of the Earth's rotation axis introduces another difference between sidereal time and solar time. This is seen in how the year is measured. A year is defined as the orbital period of the Earth. However, if you use the Sun's position as a guide, you come up with a time interval about 20 minutes shorter than if you use the stars as a guide. The time required for the constellations to complete one 360° cycle around the sky and to return to their original point on our sky is called a sidereal year. This is the time it takes the Earth to complete exactly one orbit around the Sun and equals 365.2564 solar days.
The slow shift of the star coordinates from precession means that the Sun will not be at exactly the same position with respect to the celestial equator after one sidereal year. The tropical year is the time interval between two sucessive vernal equinoxes. It equals 365.2422 solar days and is the year our calendars are based on. After several thousand years the 20 minute difference between sidereal and tropical years would have made our summers occur several months earlier if we used a calendar based on the sidereal year.
| local noon | sidereal day | sidereal year |
|---|---|---|
| tropical year |
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: January 18, 2022