The velocity of stars are determined by using the doppler effect
(see the doppler effect section).
The motion of a star
causes a shift in the wavelengths received. The star emits the
same spectrum it would emit if it was at rest. The pattern of lines depends on
the internal physics of the star itself. The doppler effect depends on the
external property of the star's motion through space relative to us. The
wavelength shift ![]() =
= ![]() new -
new -
![]() rest, where
rest, where
![]() new is the observed
wavelength and
new is the observed
wavelength and ![]() rest
is the wavelength you would observe if the star was not moving
relative to us. The amount of the shift depends on the velocity of the star
in this way:
rest
is the wavelength you would observe if the star was not moving
relative to us. The amount of the shift depends on the velocity of the star
in this way: ![]() /
/
![]() rest =
(radial velocity) / c, where c is the speed of light and
the radial velocity is the component of the star's motion that is
along the line of sight. Rearranging the terms you find
the radial velocity = (
rest =
(radial velocity) / c, where c is the speed of light and
the radial velocity is the component of the star's motion that is
along the line of sight. Rearranging the terms you find
the radial velocity = (![]() /
/
![]() rest) × c.
rest) × c.
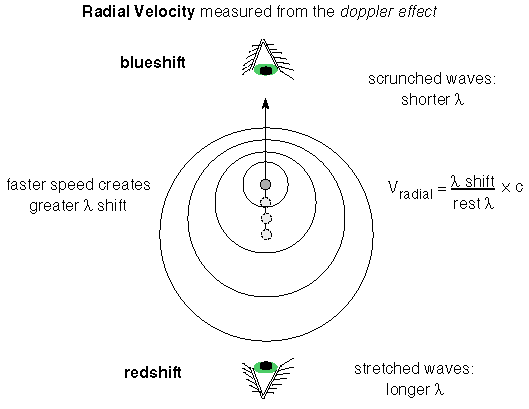
If the star is moving away from you, then you see the wavelengths stretched
out and ![]() is a positive number. The
spectral lines appear shifted to the red end of the spectrum, so the
shift is called a redshift. If the star is moving toward you, then the
wavelengths appear to the compressed and
is a positive number. The
spectral lines appear shifted to the red end of the spectrum, so the
shift is called a redshift. If the star is moving toward you, then the
wavelengths appear to the compressed and ![]() is a negative number. The spectral lines are shifted to the
blue end of the spectrum, so the shift is called a blueshift. The
doppler effect tells you only about the motion relative to you. If you move
toward the star or it moves toward you, the doppler effect will be the same. The
Earth is in motion relative to the star because it are orbiting the Sun, so
you have to take the Earth's orbital motion into account when figuring the
star's velocity from the doppler effect.
is a negative number. The spectral lines are shifted to the
blue end of the spectrum, so the shift is called a blueshift. The
doppler effect tells you only about the motion relative to you. If you move
toward the star or it moves toward you, the doppler effect will be the same. The
Earth is in motion relative to the star because it are orbiting the Sun, so
you have to take the Earth's orbital motion into account when figuring the
star's velocity from the doppler effect.
Also, the doppler effect gives you only the speed along the line of sight. Most stars move at an angle to our line of sight. The part of a star's total velocity that is perpendicular to the line of sight is called the tangential velocity.
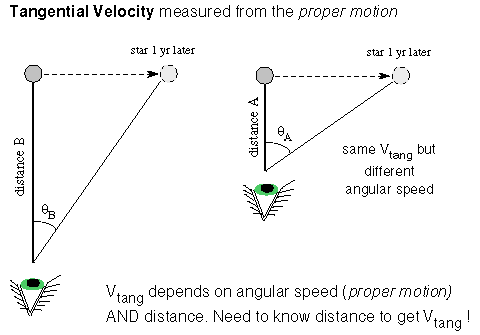
To get the tangential velocity, you need to first measure the angular
velocity of the
star across the sky (d![]() /dt). This
is how many degrees on the sky the
star moves in a given amount of time and is called the proper motion
by astronomers. If you determine the star's distance
from its trigonometric parallax or the inverse square law method, you can
convert the angular velocity (proper motion) to tangential velocity in physical
units such as kilometers/second.
The tangential velocity = k × the star's distance ×
the proper motion, where k is a conversion factor that will
take care of the conversion from arc seconds and parsecs and years to kilometers/second.
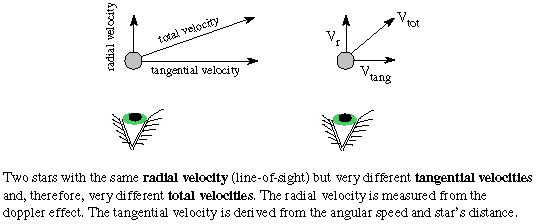
Using the Pythagorean theorem for right triangles, you find that the star's
total velocity = Sqrt[(radial velocity)2 +
(tangential velocity)2].
/dt). This
is how many degrees on the sky the
star moves in a given amount of time and is called the proper motion
by astronomers. If you determine the star's distance
from its trigonometric parallax or the inverse square law method, you can
convert the angular velocity (proper motion) to tangential velocity in physical
units such as kilometers/second.
The tangential velocity = k × the star's distance ×
the proper motion, where k is a conversion factor that will
take care of the conversion from arc seconds and parsecs and years to kilometers/second.
Using the Pythagorean theorem for right triangles, you find that the star's
total velocity = Sqrt[(radial velocity)2 +
(tangential velocity)2].
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 18, 2022