Video lecture for this page
This material (including images) is copyrighted!.
See my copyright notice for fair use
practices.
Observations of the stars in all regions of the electromagnetic spectrum
and careful observations of the Sun's pulsation modes and neutrinos provide the
data needed to construct models of the interiors of stars.
This section is about how to find out what the interior of a star is like
without physically taking one apart (a rather difficult thing to do).
Astronomers construct mathematical models of the interior of a star using the
information pouring from the surfaces of stars (especially the Sun) and their
knowledge of how gases behave under different conditions. The
mathematical models are a set of equations that describe how things work
layer by layer in a star. Fortunately, the interior of stars is completely
gaseous all the way to the center, so the equations are relatively simple
(whew!). The physics of gases can be described with just three parameters:
- Temperature---a measure of the random motion
energy (the average kinetic energy) of the gas particles. The higher the
temperature, the more random kinetic energy is present.
- Pressure---the amount of force/area. Hot gas expands to
create pressure on its surroundings. For example, the gas inside a hot air balloon
pushes out on the material of the balloon enclosing the gas.
- Mass Density---the amount of mass/volume. Gaseous
material can be compressed to smaller volumes and higher densities.
How the three parameters work together to describe the material you are studying
is determined by the equation of state of the material. This is an
equation that relates density, pressure, and temperature. The equation of state
for solids and liquids is very complex and uncertain. The equation of state for
the gas is
simple: the pressure = (a constant × the mass density × the
temperature) / (the molecular weight of the gas). The molecular weight
of a particular type of gas is the combined mass of all of the isotopes of that
type of gas in the proportions found in nature. For hydrogen, the molecular weight
is very close to 1; for helium, the molecular weight is very close to 4. For
a gas made of different types of atoms (such as that found in stars), the molecular
weight is the weighted mean of the different atomic types, taking into account
the relative proportions of the different types of atoms. This equation of state
for simple gases is also called the ideal gas law.
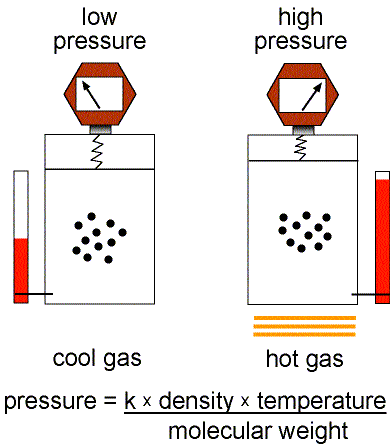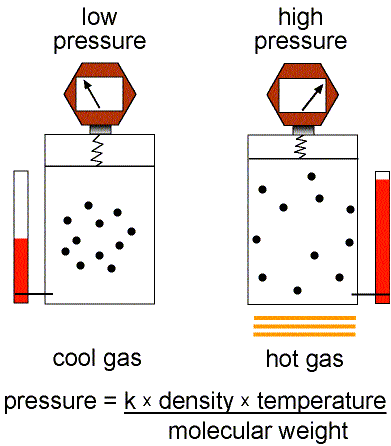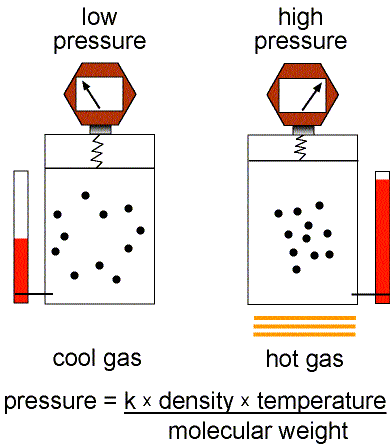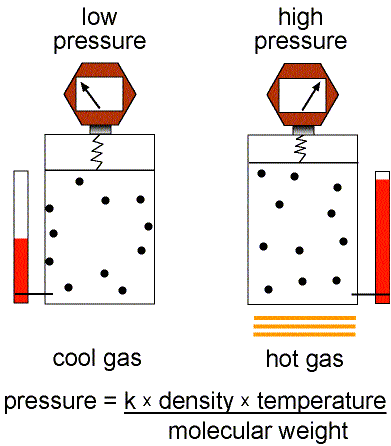
Stars are held together by gravity. Gravity tries to compress everything to the
center. What holds an ordinary star up and prevents total collapse is thermal and
radiation pressure. The thermal and radiation
pressure tries to expand the star layers outward to infinity.
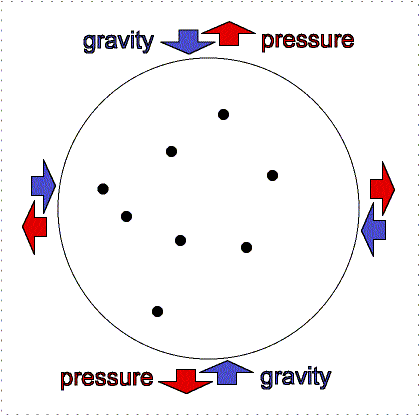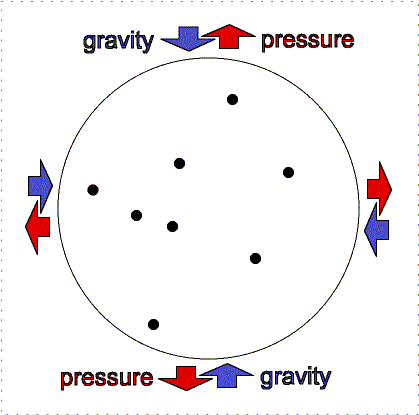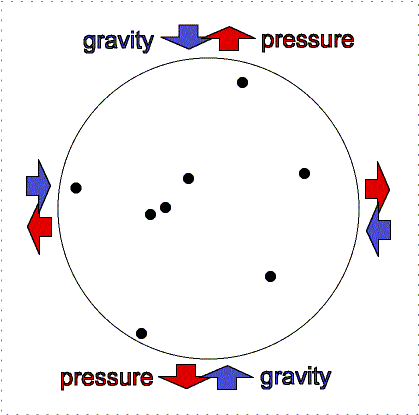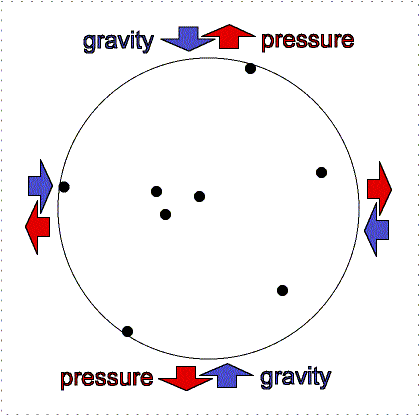
Hydrostatic
equilibrium: gravity compression is balanced by pressure outward. |
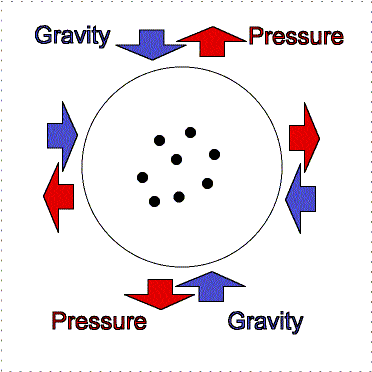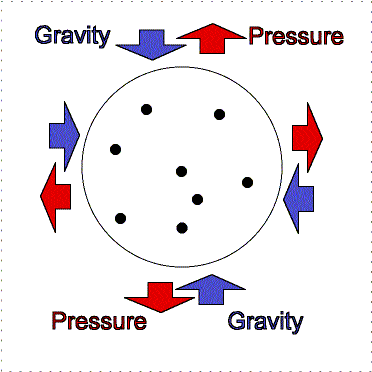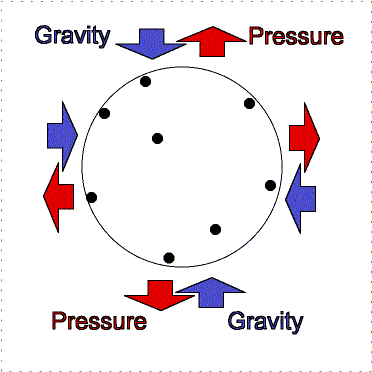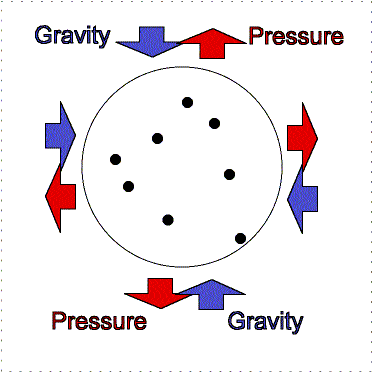
Greater gravity
compresses the gas, making it denser and hotter, so the outward pressure increases. |
In any given layer of a star,
there is a balance between the thermal pressure (outward) and the weight of the
material above pressing downward (inward). This balance is called
hydrostatic equilibrium. A star is like a balloon. In a balloon the gas
inside the balloon pushes outward and the elastic material supplies just
enough inward compression to balance the gas pressure. In a star the star's internal
gravity supplies the inward
compression. Gravity compresses the star into the most compact shape possible: a
sphere. Stars are round because gravity attracts everything in an object to the
center. Hydrostatic equilibrium also explains why the Earth's atmosphere does not
collapse to a very thin layer on the ground and how the tires on your car or
bicycle are able to support the weight of your vehicle.
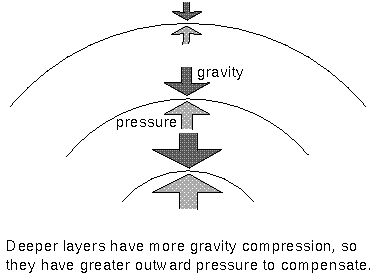
Long before astronomers knew about nuclear fusion, they had a good idea of how the density
and temperature of stars increased toward their cores. Deeper layers
have more gravity compression from the overlying layers. The greater
gravity compression raises the density of the gas. In order to balance the
greater gravity compression, the outward pressure of the gas and radiation is
increased by raising the temperature. Calculating the change in density and
temperature layer by layer toward the center of a star, you find the
temperature at the core of a star = 8 to 28 million K and the densities = 10 to
130 times the density of water. As stars age, these numbers increase! You have
already seen in the
previous section that
hydrostatic equilibrium also provides a ``thermostatic control'' on the energy
generation inside a star and keeps the star stable.
Other basic physical principles are put into the mathematical models:
- Continuity of Mass: the total stellar mass =
sum of all of the shell
layer masses. Mass is distributed smoothly throughout star's interior (there
are no gaps or pockets of ``negative'' mass). Also, the law of the
conservation of mass says that the total amount of mass does not change with time.
- Continuity of Energy: the amount of energy flowing
out the top of
each shell layer in a star = the amount of energy flowing in at bottom of the
shell layer. No energy is magically destroyed or created from nothing. A star's
luminosity = sum of all of the shell layer energies. Also, the law of the
conservation of energy says that the total amount of energy does not change with
time. Energy can change from one form to another form of energy, but the total
amount is a constant.
- Energy Transport: Recall from the discussion
about how energy flows
in planetary atmospheres that energy moves from hot to cold via conduction,
radiation, or convection. Nature will first try to use radiation (photons) to
move energy from the very hot interior to the very cold space. If radiation
cannot transport all of the energy over the distance from the center to the
surface of the star, then nature will also use convection. Convection is the
bulk motion of gases used to transport energy. Hot gases rise to the upper levels
and radiate their extra energy at the upper levels while cooler gases sink to
pick up more energy from the hot interior. Conduction transports energy by
having each atom transfer its energy to the atom next to it. Conduction is not
an efficient process in a gas so it transports a very small amount of energy in
stars and is usually ignored.
- Opacity: It takes a LONG time for photons produced
by nuclear
reactions in the core to reach the surface. In the opaque interior a photon
travels only about 1 centimeter before it runs into an atom or ion and is
absorbed. A measure of the gas' ability to absorb the photons is called its
opacity. You cannot see into the interior of a star because the gas has a
high opacity.
The photon is later re-emitted but in a random direction. It may be
re-emitted in the direction it came from! So the photon travels a very zig-zag
sort of path outward. It takes about a million years for a photon to travel
from where it was created in the core to the surface where it is finally released
into space. Along the way the photon has transferred some its energy to the
gas particles, so the photon has changed from very high energy gamma rays to the
lower energy visible light photons. Some of the radiation is also in the form of
neutrinos. The gas has almost zero opacity with the neutrinos so they pass right
on through the star's gas in just a few seconds.
- The equation of state, hydrostatic equilibrium and the other physical
principles are put together for each layer in a star. The equations are solved
for each layer starting from the layer there is direct information of, the
surface. That result gives the conditions for the next layer's equations. Solving
the layer's equations gives the conditions for the layer below it and this process
continues on down toward the center layer by layer. In order to get sufficient
detail for accurate results, the star's interior is divided into hundreds of layers.
To save on time, the equations are solved using a computer.
 Go back to previous section --
Go back to previous section --
 Go to next section
Go to next section
last updated:
June 19, 2022
Is this page a copy of Strobel's
Astronomy Notes?
Author of original content:
Nick Strobel





![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section