Powers of a Telescope

Chapter index in this window —   — Chapter index in separate window

Video lecture for this chapter

This material (including images) is copyrighted!. See my copyright notice for fair use practices.

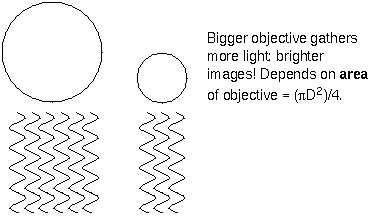
There are three features of a telescope that enable them to extend the power of our vision: a telescope's superior light-gathering ability enables us to see faint objects, a telescope's superior resolving power enables us to see even the tiniest of details, and the magnification power enables us to enlarge tiny images. Department stores and camera shops which do not know anything about telescopes, loudly proclaim their telescope's magnifying power. Magnification is the least important power of a telescope. Amateur and professional astronomers know that the light-gathering power and resolving power are the most important. These two abilities depend critically on the objective, so they make sure the optics of the objective are excellent.

Light-Gathering Power

The ability of a telescope to collect a lot more light than the human eye, its light-gathering power, is probably its most important feature. The telescope acts as a ``light bucket'', collecting all of the photons that come down on it from a far away object. Just as a bigger bucket catches more rain water, a bigger objective collects more light in a given time interval. This makes faint images brighter. This is why the pupils of your eyes enlarge at night so that more light reaches the retinas.
day pupil night pupil
Very far away, faint objects can be seen only with BIG objective telescopes. Making faint images brighter is critical if the light is going to be dispersed to make a spectrum.

The area of the objective is the determining factor. Since most telescope objectives are circular, the area = pi× (diameter of objective)2/4, where the value of pi is approximately 3.1416. To compare light-gathering powers of two telescopes, you divide the area of one telescope by the area of the other telescope. For example: a 40-centimeter mirror has four times the light-gathering power as a 20-centimeter mirror: [(pi402/4) / (pi202/4) = (40/20)2 = 4].

light-gathering power depends on area

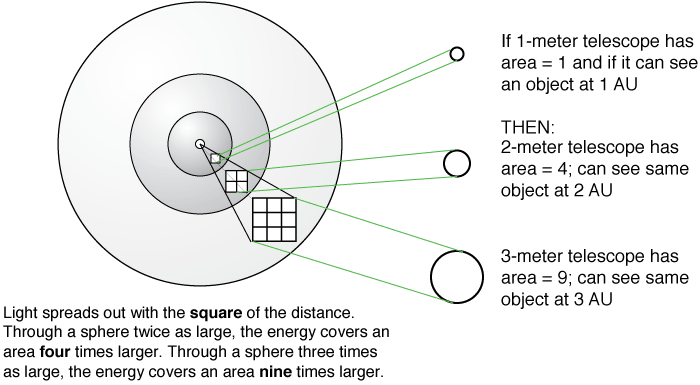
The light from a glowing object becomes more dilute as it spreads out from the object in a predictable way. The light covers larger and larger concentric spheres centered on the object, so that the object appears dimmer with the square of the distance. An object will appear four times dimmer when it is twice as far away, it will appear nine times dimmer when it is three times as far away, etc. Since the light-gathering power depends on the square of the diameter of the objective, the distance that an object can be detected increases as just the diameter of the objective (no square). To compare how much farther one telescope can detect an object than another telescope, you divide the diameter of one telescope by the diameter of the other telescope. Some examples are given in the figure below. Consider another example of how much farther one could see with the 10-meter Keck telescope than with the human eye. The largest the pupil of the eye can dilate is 9 mm (for a young eye---older eyes do not dilate as much). So the Keck telescope at 10 meters x 1000 mm/meter = 10,000 mm across can see an object at least 10,000/9 = 1111 times farther away than with the unaided, dark-adapted eye for the same exposure time. For the human eye, the exposure time is about one-tenth of a second: that is the refresh rate of an image on the retina. Longer exposures enable a telescope to detect objects at even greater distances.

Inverse square law and the detectable distance

previousGo back to previous section -- next Go to next section

Go to Astronomy Notes home

last updated: January 19, 2022

Is this page a copy of Strobel's Astronomy Notes?
Author of original content: Nick Strobel