Video lecture for this chapter
This material (including images) is copyrighted!.
See my copyright notice for fair use
practices.
Now I will apply Newton's laws of motion and gravity to topics more astronomical:
objects moving around other objects. What kinds of things can you find out about
celestial objects from just observing their motions?
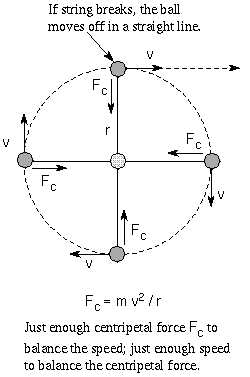Newton's first law of motion says that an object's inertia will keep it
from changing its speed and/or direction unless some force acts on it. This
means that satellites orbiting the Earth must be feeling some force that
constantly deflects them toward the center of the Earth. If there was no force,
they would travel in a straight line at a constant speed.
If you whirl a ball attached to string around your head, it moves in a circular
path around you because the string is always pulling the ball directly toward
the hand grabbing the string. The ball wants to move in a straight line and the
string is pulling it directly inward. The resulting deflection is a compromise:
a circular path. The string is applying a centripetal force to the ball:
an inward force. If you let go of the string, there is no centripetal force and
the ball will fly off in a straight line because of its inertia. If you do not
whirl the ball fast enough it will move inward to a smaller non-circular path
around you. If you whirl the ball too fast, you may not be able to give it
enough centripetal force to keep it in a circular path around you.
The amount of centripetal force needed to balance an object's inertia and keep
it in a circular path of radius r is found from Newton's second law:
the centripetal force = m v2 / r, where v and m are
the object's speed and mass, respectively. The radius of the orbit r is the same
as the distance between the moving object and the central body.
Now for orbits! Satellites are not being deflected by strings but by gravity.
Gravity provides the centripetal force needed to keep the satellites in orbit.
If you focus on the simple case of circular orbits, you can use the centripetal
force formula above with the law of gravity to determine the mass of a
planet or star. Simply set the force of gravity equal to
the centripetal force and solve for the mass of the planet or star, M.
The satellite mass m cancels out from both sides and if you put M on one
side and the rest on the other side of the equation, you get
This assumes that the satellite's mass, m, is much less than the
central object's mass so you can ignore the acceleration of the central object
toward the satellite!
How do you do that?
Let's use this result to get an estimate of the mass of the Sun. You need to use
something orbiting with a known radius and speed. The Earth's orbit
is roughly circular with radius = 1.5 × 1011
meters and the Earth moves with a speed 30,000 meters/second (= 30 km/s) in its orbit.
The distance is given in meters to match the units of the speed. The distance unit of
a meter is used because you will be using the gravitational constant G in your
calculation and it uses the meter unit. When you do a calculation, you must be sure you
check that your units match up or you will get nonsense answers.
Plug the values into the mass relation:
the Sun's mass = (30,000)2 × (1.5 ×
1011)/(6.7 × 10-11) = 2 × 1030 kilograms.
This is much larger than the
Earth's mass so it was okay to ignore the Sun's movement toward the Earth.
Using no approximations (ie., not assuming a circular orbit and including the
Sun's motion toward the Earth) gives a value for the Sun's mass that is very
close to this. Your answer does not depend on which planet you choose to use (here
you used the Earth's orbit). You would get the same value for the mass of the Sun
if you had used any of the other planets orbital speeds and sizes.
|
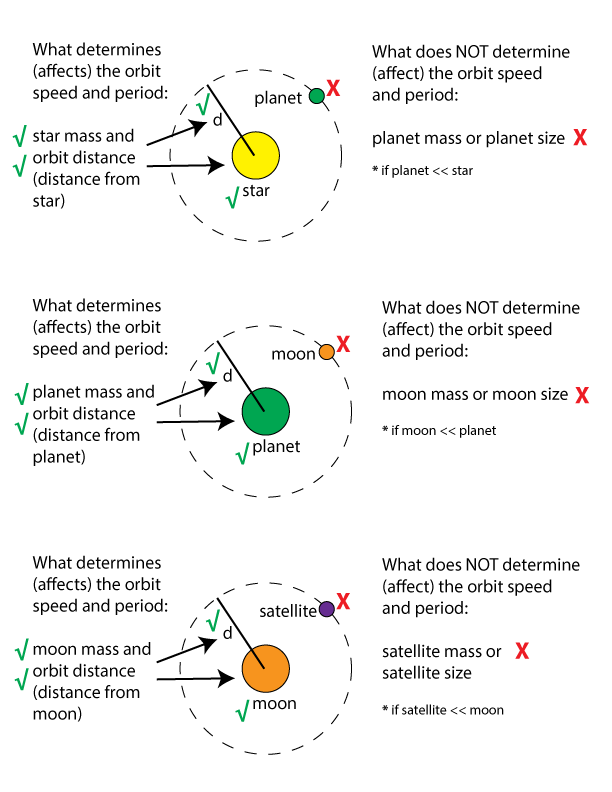
This relation tells you what you need to know in order to measure a planet's or
star's mass:
the orbital speed of a satellite and the distance it is from the center of the
planet or star. Because the velocity is on top of the fraction, satellites
are made to move faster if the mass of the central object is greater. At the
same distance, a massive
planet will exert more gravity force than a low-mass planet, so the
massive planet will produce greater inward accelerations on satellites orbiting it.
The satellites will, therefore, orbit at faster speeds.
Sometimes the orbital period P is measured
instead of the orbital velocity. The orbital period is the time it takes the object to
travel the circumference of its orbit (for a circle, the circumference =
2pr, where
p is
approximately 3.1416). Recall that speed = (distance travelled)/time,
so the speed v = the circumference of the orbit/orbital period. When you
substitute this for the speed in the mass relation above, you get
This may look familiar to you---it is Kepler's third law! There is a distance
cubed, an orbital period squared, and some other constant factors. Newton found
that when Kepler used the motions of the planets to formulate his third law, Kepler
was actually measuring the mass of the Sun. If you use the convenient set of
units of an astronomical unit for the distance, a year for the time, and a
``solar mass'' (mass relative to the Sun) for the mass, the complicated term
(4p2)/G becomes the simple value of 1. For
the planets orbiting the Sun, the mass relation becomes 1 = r3 /
P2, or r3 = P2, just
what Kepler found.
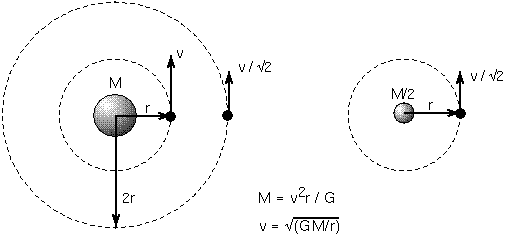The mass formula above tells you that satellites orbiting massive planets must
move faster than satellites orbiting low-mass planets at the same distance.
Massive planets have stronger gravity than low-mass planets so a satellite
orbiting a massive planet is accelerated by a greater amount than one going
around a lesser mass planet at the same distance. To balance the stronger inward
gravitational pull of the massive planet, the satellite must move faster in its
orbit than if it was orbiting a lesser mass planet. Of course, this also applies
to planets orbiting stars, stars orbiting other stars, etc.
If you solve for the orbit speed, v, in the mass formula, you
can find how fast something needs to move to balance the inward pull of gravity:
v2 = (G M)/r .
Taking the square root of both sides (you want just v not
v2), you get
v = Sqrt[(G M)/r].
How do you do that?
Find the orbital speed of Jupiter around the Sun. Jupiter's distance from
the Sun is 5.2 A.U., or 7.8×1011 meters and the Sun's mass is
2×1030 kilograms.
The orbital speed of Jupiter around the Sun is
Sqrt[6.7×10-11 ×
(2×1030)/(7.8×1011)] =
Sqrt[1.718×108] = 1.3×104 meters/second,
or 13 kilometers/second. What do you think you wouldd find if you used one of the Trojan
asteroids, millions of times less massive than Jupiter, that orbits the Sun at 5.2 A.U.?
|
Notice that the orbital speed v (and therefore, the orbital period P) does not depend on the mass of the satellite! The mass M in the formula above is the mass of the central object. If we consider the Sun-Jupiter-Trojan asteroid example in the "How do you do that?" box above (and recall the discussion in the Gravitational Acceleration section), the Sun-Jupiter gravity force is MUCH greater than the Sun-Trojan asteroid gravity force but Jupiter has much greater inertia (resistance to change = mass). The greater gravity force between the Sun and Jupiter is compensated for by the greater inertia of Jupiter so the acceleration of Jupiter will be the same as the acceleration of the Trojan asteroid---Jupiter and the Trojan asteroid will have the same orbital velocity and same orbital period.
If an object moves fast enough it can escape a massive object's gravity and
not be drawn back toward the massive object. The critical speed needed to do
this is the escape velocity. More specifically, this is the initial
speed something needs to escape the object's gravity and assumes that there is no
other force acting on the
object besides gravity after the initial boost. Rockets leaving the Earth do
not have the escape velocity at the beginning but the engines provide thrust
for an extended period of time, so the rockets can eventually escape. The concept
of escape velocity applies to anything
gravitationally attracted to anything else (gas particles in planet
atmospheres, comets orbiting the Sun, light trying to escape from black holes,
galaxies orbiting each other, etc.).
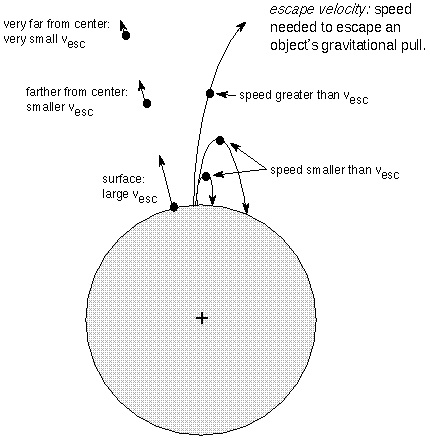
Using Newton's laws of motion and law of gravity, you can find that the escape
velocity vesc looks very similar to the orbital speed:
vesc = Sqrt[(2 G M)/r].
This is a factor
Sqrt[2] larger than the circular orbital speed.
Since the mass M is on top of the fraction, the escape velocity
increases as the mass increases. More massive bodies exert greater gravity
force, so escaping objects have to move faster to overcome the greater gravity.
Also, the distance from the center of the object r is in the bottom of the
fraction, so the escape velocity DEcreases as the distance increases. Gravity
decreases with greater distance, so objects farther from a massive body do not need to
move as quickly to escape it than those closer to it.
How do you do that?
Find the escape velocity from the surface of the Earth.
Using the
acceleration of gravity, you can find that the Earth has a mass
of 6.0×1024 kilograms. The Earth's radius is 6.4×106
meters. Since the mass and distance from the center are in the standard units, you just
need to plug their values into the escape velocity relation.
The Earth's surface escape velocity is
Sqrt[2× (6.7×10-11) × (6.0×1024)/
(6.4×106)] = Sqrt[1.256×108] =
1.1×104 meters/second (= 11 km/s). Here are some other surface
escape velocities: Moon = 2.4 km/s, Jupiter = 59.6 km/s, Sun = 618 km/s.
|
Vocabulary
| centripetal force | escape velocity |
Formulae
- Mass of central object = [(orbital speed)2 × distance)/G.
- Mass of central object (Kepler's 3rd law) = (4p2)/G
× [(distance)3/(orbital period)2].
- Orbital speed = Sqrt[G × Mass / distance].
- Escape velocity = Sqrt[2G × Mass / distance].
- What keeps satellites orbiting the Earth moving along their curved paths?
- What two things must be determined first in order to calculate the mass of a
planet or a star?
- Jupiter's moon Io has about the same mass as the Moon and orbits Jupiter at
about the same distance that the Moon orbits the Earth (center to center). Then
why does Io take only 1.8 days to orbit Jupiter but our Moon takes 27.3 days to
orbit the Earth?
- Astronomers were able to accurately measure the orbital periods of the moons
of Jupiter since the time of Galileo, so why was an accurate value for Jupiter's
mass not found for over 300 years until the astronomical unit was measured
accurately?
- Which would have a shorter orbital period, a planet orbiting a massive
star at 3 A.U. or a planet orbiting a low-mass star at 3 A.U.? Explain your answer.
- If a planet orbiting a massive star has the same orbital period as a
planet orbiting a low-mass star, which of the planets orbits at a greater distance
from its star? Explain your answer.
- What two things does the escape velocity depend on?
- Why does the planet Saturn with over 95 times the Earth's mass have a
smaller escape velocity at its cloudtops than the Earth has at its cloudtops?
- Why is Jupiter's escape velocity at its
cloudtops over two times higher than the Earth's surface escape
velocity, even
though Jupiter has a much larger diameter than the Earth?
Go back to previous section --
Go to next section
last updated:
February 21, 2022
Is this page a copy of Strobel's
Astronomy Notes?
Author of original content:
Nick Strobel