Video lecture for this chapter
This material (including images) is copyrighted!.
See my copyright notice for fair use
practices.
Kepler's third law of planetary motion says that the average distance of a
planet from the Sun cubed is directly proportional to the orbital
period squared. Newton found that his gravity force law could explain Kepler's
laws. Since Newton's law of gravity applies to any object with mass, Kepler's
laws can be used for any object orbiting another object. Let's look at
satellites orbiting a planet.
If you have two satellites (#1 and #2) orbiting a planet, Kepler's third law
says:
(period #1/period #2)2 = (distance #1/distance #2)3,
where the distance is the average distance of the
satellite from the planet---the orbit's semimajor axis. The satellites must be
orbiting the same planet in order to use Kepler's third law! Kepler found this law
worked for the planets because they all orbit the same star (the Sun).
If you have measured the orbital period of
one satellite around a planet, you can then easily find how long it would take
any other satellite to orbit the planet in any size oribt. Kepler's third law can
be simplified down to
| period #1 | = |
period #2 × Sqrt[(distance #1/distance #2)3] |
| OR |
|
| period #1 | = |
period #2 × (distance #1/distance #2)3/2. |
Those of you with a scientific calculator (one that does powers, trig functions,
scientific notation, etc.) will want to use the formula on the last line
(remember that 3/2 = 1.5). Those
with a calculator that just has a square root button will want to use the
formula on the second-to-last line.
If the satellite is orbiting the Sun,
then the relation can be greatly simplified with an appropriate choice of
units: the unit of years for the orbit period
and the distance unit of astronomical units. In this case, the
reference ``satellite'' is the Earth and Kepler's third law becomes
period = distance3/2. Let's use this to find out how long it takes
to explore the solar system.
The simplest way to travel between the planets is to let the Sun's gravity do
the work and take advantage of Kepler's laws of orbital motion. A fuel efficient
way to travel is to put the spacecraft in orbit around the Sun with the Earth
at one end of the orbit at launch and the other planet at the opposite end at
arrival. These orbits are called ``Hohmann orbits'' after Walter Hohmann who
developed the theory for transfer orbits. The spacecraft requires only an
acceleration at the beginning of the trip and a deceleration at the end of the
trip to put it in orbit around the other planet.
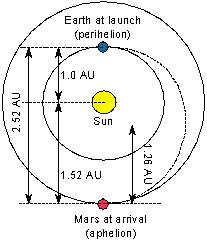 Let's
go to Mars! The relative positions of Earth and
Mars must be just right
at launch so that Mars will be at the right position to greet the spacecraft
when it arrives several months later. These good positionings happen once every
780 days (the synodic period of Mars). The spacecraft must be launched within a
time interval called the ``launch window'' that is just few of weeks long to use a
Hohmann orbit for the spacecraft's path. The Earth is at the
perihelion (point closest to the Sun) of the spacecraft orbit (here,
1.0 A.U.) and Mars is at the aphelion (point farthest from the Sun---here,
1.52 A.U.).
Let's
go to Mars! The relative positions of Earth and
Mars must be just right
at launch so that Mars will be at the right position to greet the spacecraft
when it arrives several months later. These good positionings happen once every
780 days (the synodic period of Mars). The spacecraft must be launched within a
time interval called the ``launch window'' that is just few of weeks long to use a
Hohmann orbit for the spacecraft's path. The Earth is at the
perihelion (point closest to the Sun) of the spacecraft orbit (here,
1.0 A.U.) and Mars is at the aphelion (point farthest from the Sun---here,
1.52 A.U.).
Kepler's third law relates the semi-major axis of the orbit to its sidereal
period. The major axis is the total length of the long axis of the elliptical
orbit (from perihelion to aphelion). For the Mars journey, the major axis =
1.52 + 1.0 A.U. = 2.52 A.U. The semi-major axis is one-half of the major
axis, so divide the major axis by two: 2.52/2 = 1.26 A.U. Now apply Kepler's
third law to find the orbital period of the spacecraft = 1.263/2 =
1.41 years. This is the period for a full orbit (Earth to Mars and back to Earth),
but you want to go only half-way (just Earth to Mars). Traveling from Earth to
Mars along this path will take (1.41 / 2) years = 0.71 years or about 8.5 months.
When the craft is launched, it already has the Earth's orbital velocity of
about 30 kilometers/second. Since this is the speed for a circular orbit around the Sun
at 1.0 A.U., a reduction in the spacecraft's speed would make it fall closer
to the Sun and the Hohmann orbit would be inside the Earth's orbit. Since you
want to go beyond the Earth's orbit, the spacecraft needs an increase in its
speed to put it in an orbit that is outside the Earth's orbit. It will slow
down gradually as it nears aphelion.
At aphelion the spacecraft will not be
traveling fast enough to be in a circular orbit at Mars' distance (1.52 A.U.)
so it will need to arrive at aphelion slightly before Mars does. Mars
will then catch up to it. But the spacecraft will be moving much too fast to be in
a circular orbit around Mars, so it will need to slow down to go in orbit
around Mars.
On its journey to Mars, the spacecraft's distance from the Sun is continuously
monitored to be sure the craft is on the correct orbit. Though the spacecraft
responds mostly to the Sun's gravity, the nine planets' gravitational pulls on the
spacecraft can
affect the spacecraft's path as it travels to Mars, so occasional minor firings
of on-board thrusters may be required to keep the craft exactly on track.
For more details about Hohman orbits, see the "Let's Go to Mars! Calculating Launch Windows" activity from the people who actually do it (NASA/JPL).

Vocabulary
Formulae
- Kepler's third law: period #1 = period #2 ×
Sqrt[(distance #1/distance #2)3]
- Kepler's third law: period #1 = period #2 ×
(distance #1/distance #2)3/2
- If considering objects orbiting the Sun, measure the orbit period in years
and the distance in A.U. With these units, Kepler's third law is simply:
period = distance3/2.
- How can you predict the orbital period of Jupiter's satellite Europa from
observations of the other jovian moon Io?
- If Io takes 1.8 days to orbit Jupiter at a distance of 422,000 kilometers
from its center, find out how long it would take Europa to orbit Jupiter at
671,000 kilometers from its center.
- If the Moon were twice as far from the Earth as it is now, how long could
a solar eclipse last? (Solar eclipses currently last up to about two hours from
the start of the cover-up to when the Moon no longer blocks the Sun at all.)
- The Hubble Space Telescope orbits the Earth 220 kilometers above the surface
and takes about 1.5 hours to complete one orbit. How can you find out how far
up to put a communication satellite, so that it takes 24 hours to circle the Earth?
(Such an orbit is called a ``geosychronous orbit'' because the satellite remains
above a fixed point on the Earth.)
- Why does NASA not launch interplanetary spacecraft when the planets are at
opposition (closest to the Earth)?
- Find out how long it will take the Cassini spacecraft to travel to Saturn
9.5 A.U. from the Sun.
 Go back to previous section --
Go back to previous section --
 Go to next section
Go to next section
last updated:
January 9, 2024
Is this page a copy of Strobel's
Astronomy Notes?
Author of original content:
Nick Strobel
 Let's
go to Mars! The relative positions of Earth and
Mars must be just right
at launch so that Mars will be at the right position to greet the spacecraft
when it arrives several months later. These good positionings happen once every
780 days (the synodic period of Mars). The spacecraft must be launched within a
time interval called the ``launch window'' that is just few of weeks long to use a
Hohmann orbit for the spacecraft's path. The Earth is at the
perihelion (point closest to the Sun) of the spacecraft orbit (here,
1.0 A.U.) and Mars is at the aphelion (point farthest from the Sun---here,
1.52 A.U.).
Let's
go to Mars! The relative positions of Earth and
Mars must be just right
at launch so that Mars will be at the right position to greet the spacecraft
when it arrives several months later. These good positionings happen once every
780 days (the synodic period of Mars). The spacecraft must be launched within a
time interval called the ``launch window'' that is just few of weeks long to use a
Hohmann orbit for the spacecraft's path. The Earth is at the
perihelion (point closest to the Sun) of the spacecraft orbit (here,
1.0 A.U.) and Mars is at the aphelion (point farthest from the Sun---here,
1.52 A.U.).
