Video lecture for this chapter
This material (including images) is copyrighted!.
See my copyright notice for fair use
practices.
When light is passed through a prism or a diffraction grating to produce a
spectrum, the type of spectrum you will see depends on what kind of object is
producing the light: is it a thick or thin gas, is it hot or cool, is it a gas
or a solid? There are two basic types of spectra: continuous spectrum
(energy at all wavelengths)
and discrete spectrum (energy at only certain wavelengths).
Astronomers usually refer to the two types of discrete spectra:
emission lines (bright lines) and absorption lines (dark lines
in an otherwise continuous spectrum) as different types of spectra.
A rainbow is an example of a continuous spectrum. Most continuous
spectra are from hot, dense objects like stars, planets, or moons. The continuous
spectrum from these kinds of objects is also called a thermal spectrum,
because hot, dense objects will
emit electromagnetic radiation at all wavelengths or colors. Any solid, liquid
and dense (thick) gas at a temperature above absolute zero will produce a
thermal spectrum. A thermal spectrum is the simplest type of spectrum because
its shape depends on only the temperature. A discrete spectrum is more
complex because it depends on temperature and other things like the chemical
composition of the object, the gas density, surface gravity, speed, etc.
Exotic objects like neutron stars and black holes can produce another type of
continuous spectrum called ``synchrotron spectrum'' from charged particles swirling
around magnetic fields, but I will discuss them in another chapter later on. For now,
let's look at a thermal spectrum.
Sometimes astronomers use the term ``blackbody'' spectrum for a thermal spectrum.
A ``blackbody'' is
an object that absorbs all the light falling on it, reflecting none of it,
hence, it appears black. When the ``blackbody'' object is heated, it emits
light very efficiently without any gaps or breaks in the brightness. Though
no object is a perfect ``blackbody'', most stars, planets, moons and asteroids
are near enough to being ``blackbodies'', that they will produce spectra
very similar to a perfect thermal spectrum.

Some thermal spectra for objects of different temperatures are illustrated in
the figure below.
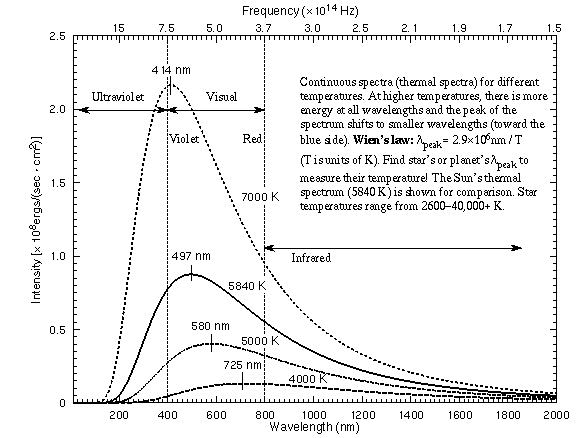
Some key features of a thermal (continuous) spectrum are as follows:
- There is light from a dense object at all possible
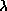 IF the object
is above 0 K (absolute zero). Since everything in the universe is
above 0 K, all dense objects (solids, liquids, thick gases) will produce a
thermal spectrum.
IF the object
is above 0 K (absolute zero). Since everything in the universe is
above 0 K, all dense objects (solids, liquids, thick gases) will produce a
thermal spectrum.
- The shape of a continuous spectrum depends on only the temperature of the
object NOT its chemical composition. This allows you to determine
the temperature of an object from a great distance away.
- As the temperature of an object increases, more light is produced at all
wavelengths than when it was cooler. You can see this effect with a light
bulb wired to a dimmer switch. As you raise the current going to the bulb,
the bulb's filament gets hotter and brighter.
- As the temperature of an object increases, the
peak of thermal spectrum curve shifts to smaller
wavelengths (higher frequencies)---cool things appear red or orange,
hotter things appear yellow or white, and very hot things blue or purple.
This is opposite to what artists use for ``cool'' colors (blues) or ``hot''
colors (reds)! You can also see this effect with the light bulb wired to a dimmer
switch. The dim bulb will have an orange color and as you make it brighter,
the bulb will turn yellow and even white.
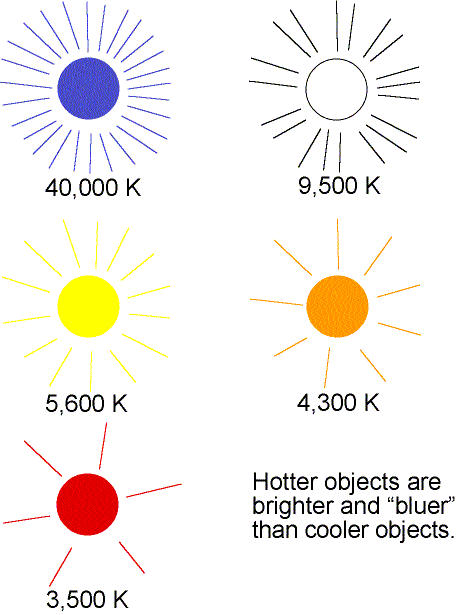
Wilhelm Wien (lived 1864--1928) discovered that the peak of the thermal
spectrum curve, 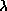 peak in nanometers,
is related to the temperature by
peak in nanometers,
is related to the temperature by
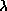 peak = 2.9 ×
106 / temperature (in K). This simple relation is now known as Wien's
Law. Using this you will find that cool objects like cars,
plants, and people radiate most of their energy in the infrared. Very cold
objects radiate mostly in the radio band.
peak = 2.9 ×
106 / temperature (in K). This simple relation is now known as Wien's
Law. Using this you will find that cool objects like cars,
plants, and people radiate most of their energy in the infrared. Very cold
objects radiate mostly in the radio band.
- A small change in the temperature produces a HUGE change in the amount
of energy emitted by every unit area of the object. If you add up all of the
energy emitted every second by an area of one square meter on the object's surface,
you find it
equals
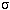 ×temperature4,
where
×temperature4,
where
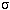 is another universal
constant of nature
[= 5.67×10-8 J/(m2 K4 s)]. This relation is called
the Stefan-Boltzmann law. Because the temperature
is raised to the fourth power, a small
rise in the temperature of an object will produce a HUGE increase in the amount of
energy it emits.
is another universal
constant of nature
[= 5.67×10-8 J/(m2 K4 s)]. This relation is called
the Stefan-Boltzmann law. Because the temperature
is raised to the fourth power, a small
rise in the temperature of an object will produce a HUGE increase in the amount of
energy it emits.
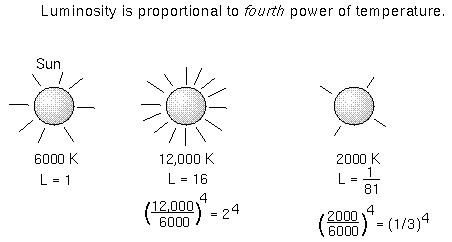
When you add up all of the energy of all of the square meters on the object's
surface, you get the luminosity---the total amount of energy emitted
every second by the object. The luminosity = (total surface area) ×
(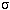 ×temperature4).
If our Sun were just twice as hot as it is now, it would produce 24
= 16 times more energy than it does now!
×temperature4).
If our Sun were just twice as hot as it is now, it would produce 24
= 16 times more energy than it does now!
The UNL Astronomy Education program's Blackbody
Curves module lets you explore
the relationship between temperature and the thermal spectrum by manipulating
various parameters with a graphical interface (link will appear in a new window).
It also introduces the concept of filters.
 Go back to previous section --
Go back to previous section --
 Go to next section
Go to next section
last updated:
January 13, 2022
Is this page a copy of Strobel's
Astronomy Notes?
Author of original content:
Nick Strobel




![]() peak in nanometers,
is related to the temperature by
peak in nanometers,
is related to the temperature by
![]() peak = 2.9 ×
106 / temperature (in K). This simple relation is now known as Wien's
Law. Using this you will find that cool objects like cars,
plants, and people radiate most of their energy in the infrared. Very cold
objects radiate mostly in the radio band.
peak = 2.9 ×
106 / temperature (in K). This simple relation is now known as Wien's
Law. Using this you will find that cool objects like cars,
plants, and people radiate most of their energy in the infrared. Very cold
objects radiate mostly in the radio band.
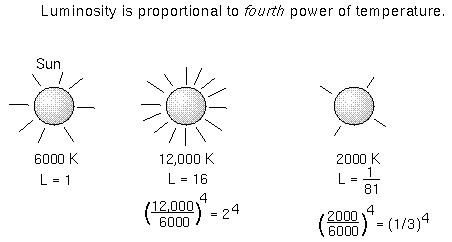
![]() ×temperature4).
If our Sun were just twice as hot as it is now, it would produce 24
= 16 times more energy than it does now!
×temperature4).
If our Sun were just twice as hot as it is now, it would produce 24
= 16 times more energy than it does now!
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section