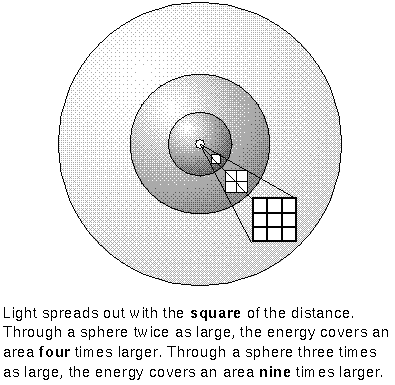
When the direct method of trigonometric parallax does not work for a star because it is too far away, an indirect method called the Inverse Square Law of Light Brightness is used. This method uses the fact that a given star will grow dimmer in a predictable way as the distance between you and the star increases. If you know how much energy the star emits (its luminosity), then you can derive how far away it must be to appear as dim as it does. Stars become fainter with increasing distance because their energy is spread out over a larger and larger surface.
A star's apparent brightness (its flux) decreases with the square of the distance. The flux is the amount of energy reaching each square centimeter of a detector (e.g., your eye, CCD, piece of the sphere) every second. Energy from any light source radiates out in a radial direction so concentric spheres (centered on the light source) have the same amount of energy pass through them every second. As light moves outward it spreads out to pass through each square centimeter of those spheres.

The same total amount of energy must pass through each sphere surface. Since a
sphere has a surface area of 4![]() ×
(its radius)2, the flux of energy on sphere-1 = (the flux of energy on
sphere #2) × [(sphere #2's radius)/(sphere #1's radius)]2. Notice that
the radius for the reference flux (sphere #2) is on the top of the fraction
while the radius for the unknown flux (sphere #1) is on the bottom---this is an inverse
square law! As the distance INcreases, the flux DEcreases with the square of the
distance. In formula form, this means the star's flux = star's luminosity / (4
×
(its radius)2, the flux of energy on sphere-1 = (the flux of energy on
sphere #2) × [(sphere #2's radius)/(sphere #1's radius)]2. Notice that
the radius for the reference flux (sphere #2) is on the top of the fraction
while the radius for the unknown flux (sphere #1) is on the bottom---this is an inverse
square law! As the distance INcreases, the flux DEcreases with the square of the
distance. In formula form, this means the star's flux = star's luminosity / (4![]() ×
(star's distance)2 ). See the math review
appendix for help on when to multiply and when to divide the distance factor.
×
(star's distance)2 ). See the math review
appendix for help on when to multiply and when to divide the distance factor.
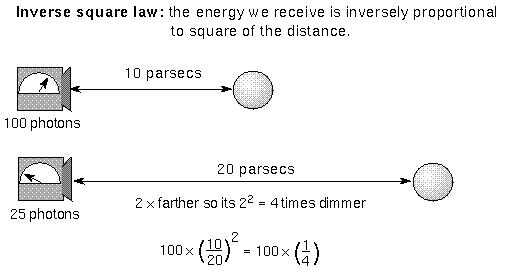
Put another way: As the flux DEcreases, the star's distance INcreases with
the square root of the flux. If you know how much energy pours through the
star's surface and you measure how much energy you detect here on the Earth,
then you can derive the star's distance from you. The star's distance = Sqrt[ (star's luminosity) / (4![]() ×
(star's flux)) ].
×
(star's flux)) ].
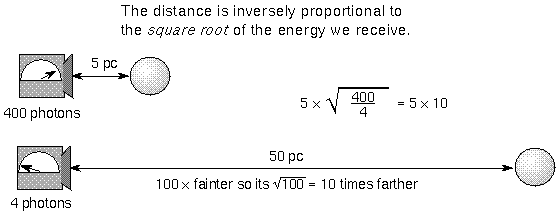
| flux | Inverse Square Law of Light Brightness | luminosity |
|---|
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 18, 2022