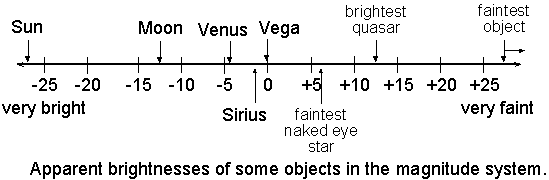
The brightness of stars are specified with the magnitude system. The Greek astronomer Hipparchus devised this system around 150 B.C.E. He put the brightest stars into the first magnitude class, the next brightest stars into second magnitude class, and so on until he had all of the visible stars grouped into six magnitude classes. The dimmest stars were of sixth magnitude. The magnitude system was based on how bright a star appeared to the unaided eye.
By the 19th century astronomers had developed the technology to objectively measure a star's brightness. Instead of abandoning the long-used magnitude system, astronomers refined it and quantified it. They established that a difference of 5 magnitudes corresponds to a factor of exactly 100 times in intensity. The other intervals of magnitude were based on the 19th century belief of how the human eye perceives differences in brightnesses. It was thought that the eye sensed differences in brightness on a logarithmic scale so a star's magnitude is not directly proportional to the actual amount of energy you receive. Now it is known that the eye is not quite a logarithmic detector.
Your eyes perceive equal ratios of intensity as equal intervals of brightness. On the quantified magnitude scale, a magnitude interval of 1 corresponds to a factor of 1001/5 or approximately 2.512 times the amount in actual intensity. For example, first magnitude stars are about 2.5122-1 = 2.512 times brighter than 2nd magnitude stars, 2.512×2.512 = 2.5123-1 = 2.5122 times brighter than 3rd magnitude stars, 2.512×2.512×2.512 = 2.5124-1 = 2.5123 times brighter than 4th magnitude stars, etc. (See the math review appendix for what is meant by the terms ``factor of'' and ``times''.) Notice that you raise the number 2.512 to a power equal to the difference in magnitudes.
Also, many objects go beyond Hipparchus' original bounds of magnitude 1 to 6. Some very bright objects can have magnitudes of 0 or even negative numbers and very faint objects have magnitudes greater than +6. The important thing to remember is that brighter objects have smaller magnitudes than fainter objects. The magnitude system is screwy, but it's tradition! (Song from Fiddler on the Roof could be played here.)
How do you do that?Star A has an apparent magnitude = 5.4 and star B has an apparent magnitude = 2.4. Which star is brighter and by how many times? Star B is brighter than star A because it has a lower apparent magnitude. Star B is brighter by 5.4 - 2.4 = 3 magnitudes. In terms of intensity star B is 2.512(5.4-2.4) = 2.5123.0 = approximately 15.8 times brighter than star A. The amount of energy you receive from star B is almost 16 times greater than what you receive from star A. |
A star can be luminous because it is hot or it is large (or both!). The luminosity of
an object = the amount of energy every square meter produces multiplied by its surface
area. Recall from the
electromagnetic radiation
chapter that the amount
of energy pouring through every square meter =
× (object's surface
temperature)4, where
is the Stefan-Boltzmann constant. Because the temperature is raised to the fourth power,
it means that the luminosity of a star increases very quickly with even slight increases
in the temperature.
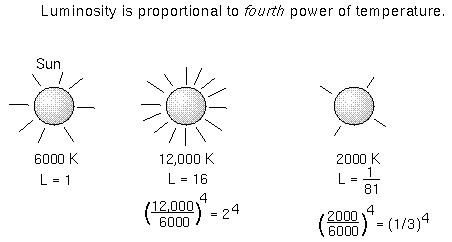
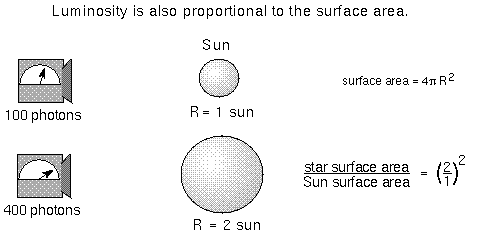
Because the surface area is also in the luminosity relation, the luminosity of a bigger star is larger than a smaller star at the same temperature. You can use the relation to get another important characteristic of a star. If you measure the apparent brightness, temperature, and distance of a star, you can determine its size.
The figure below illustrates the inter-dependence of measurable quantities with the derived values that have been discussed so far. In the left triangular relationship, the apparent brightness, distance, and luminosity are tied together such that if you know any two of the sides, you can derive the third side. For example, if you measure a glowing object's apparent brightness (how bright it appears from your location) and its distance (with trigonometric parallax), then you can derive the glowing object's luminosity. Or if you measure a glowing object's apparent brightness and you know the object's luminosity without knowing its distance, you can derive the distance (using the inverse square law). In the right triangular relationship, the luminosity, temperature, and size of the glowing object are tied together. If you measure the object's temperature and know its luminosity, you can derive the object's size. Or if you measure the glowing object's size and its temperature, you can derive the glowing object's luminosity---its electromagnetic energy output.
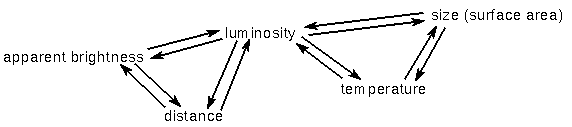
Finally, note that a small, hot object can have the same luminosity as a large, cool object. So if the luminosity remains the same, an increase in the size (surface area) of the object must result in a DEcrease in the temperature to compensate.
Most famous apparently bright stars are also intrinsically bright (luminous). They can be seen from great distances away. However, most of the nearby stars are intrinsically faint. If you assume we live in a typical patch of the Milky Way Galaxy (using the Copernican principle), then you deduce that most stars are puny emitters of light. The bright stars you can see in even the city are the odd ones in our galaxy! The least luminous stars have absolute magnitudes = +19 and the brightest stars have absolute magnitudes = -8. This is a huge range in luminosity! See the ``How do you do that?'' box below the following table for examples of using the apparent and absolute magnitudes to determine stellar distances and luminosities of stars.
Even the intrinsically faintest star's luminosity is much, much greater than all of the power we generate here on the Earth so a "watt" or a "megawatt" are too tiny a unit of power to use for the stars. Star luminosities are specified in units of solar luminosity---relative to the Sun (so the Sun generates one solar luminosity of power). One solar luminosity is about 4 × 1026 watts.
Magnitudes and Distances for some well-known Stars (from the
precise measurements of the Hipparcos mission)
| Star | App.Mag.* | Distance(pc) | Abs.Mag.* | Visual Luminosity(rel. to Sun)** |
|---|---|---|---|---|
| Sun | -26.74 | 4.84813×10-6 | 4.83 | 1 |
| Sirius | -1.44 | 2.6371 | 1.45 | 22.5 |
| Arcturus | -0.05 | 11.25 | -0.31 | 114 |
| Vega | 0.03 | 7.7561 | 0.58 | 50.1 |
| Spica | 0.98 | 80.39 | -3.55 | 2250 |
| Barnard's Star | 9.54 | 1.8215 | 13.24 | 1/2310 |
| Proxima Centauri | 11.01 | 1.2948 | 15.45 | 1/17700 |
*magnitudes measured using ``V'' filter, see the next section.
**The visual luminosity is the energy output in the ``V'' filter. A total luminosity (``bolometric luminosity'') would encompass the energy in all parts of the electromagnetic spectrum.
How do you do that?A quantity that uses the inverse square law and the logarithmic magnitude system is the ``distance modulus''. The distance modulus = the apparent magnitude - absolute magnitude. This is equal to 5 × log(distance in parsecs) - 5. The ``log()'' term is the ``logarithm base 10'' function (it is the ``log'' key on a scientific calculator). If you measure a star's apparent magnitude and its distance from its trigonometric parallax, the star's absolute magnitude = the apparent magnitude - 5 × log(distance + 5. For example, Sirius has an apparent magnitude of -1.44 and Hipparcos measured its distance at 2.6371 parsecs, so it has an an absolute magnitude of -1.44 - 5×log(2.6371) + 5 = -1.44 - (5×0.421127) + 5 = 1.45.
If you know a star's absolute magnitude, then when you compare it to calibration stars,
you can determine its distance.
For example, Spica has an apparent magnitude of 0.98 and stars of its type have absolute magnitudes of about -3.55, so Spica is at a distance of 10[0.98 - (-3.55) + 5]/5 = 101.906 = 80.54 which is very close to the trig. parallax value measured by Hipparcos (Spica's absolute magnitude of -3.546 was rounded to -3.55 in the table above). If you know two star's absolute magnitudes, you can directly compare their luminosities. The ratio of the two stars' luminosities is (Lum.*1)/(Lum.*2) = 10-0.4(abs mag*1 - abs mag*2) or in an approximate relation: Lum.*1/Lum.*2 = 2.512(abs mag*2 - abs mag*1). Remember the more luminous star has an absolute magnitude that is less than a fainter star's absolute magnitude! Try out this relation on the stars given in the table above. |
Go back to previous section --
Go to next section
last updated: June 18, 2022