
The Sun produces a lot of light every second and it has been doing that for billions of years. How does it or any other star produce so much energy for so long? This section will cover how stars produce their energy. Astronomers have known for a long time that the Sun produces a tremendous amount of energy. The first part of this section will try to give you an idea of how much energy it produces. Do not feel bad if you have trouble grasping the amount. It is mind-boggling! There are several ways to generate the amount of energy coming from the Sun. What distinguishes the correct explanation from the other models is how long it can power the Sun.
To find out how long the Sun would last, you need to find out how much energy the Sun has stored in its account and know how fast it makes withdrawals on its account. The amount of time it would last is the amount of energy stored divided by the rate of withdrawal: lifetime = energy stored/consumption rate = E stored/Luminosity. Makes sense, yes? If the Sun could use all of its hydrogen to make water, the chemical reactions would only power the Sun for about 18,000 years. However, the amount of oxygen is much less than the hydrogen, so the chemical reactions can power the Sun for only 30 years.
We need a reaction with a higher efficiency. How about the ultimate in efficiency---a complete matter to energy conversion with 100% efficiency. Such a reaction could power the Sun for 1013 years. Unfortunately, there are problems with this because the number of heavy particles (protons + neutrons) in the Sun must stay the same and protons are extremely stable---they do not spontaneously change into energy (photons).
Until the beginning of this century, this was the idea physicists strongly argued for. This gravitational energy (with an efficiency of 1/10000 of one percent) could power the sun for 30 million years---a nice long time except for the nagging but ever louder criticism of the biologists who needed more time for evolution to occur and the geologists who preferred the idea of an unlimited age for the Earth but would stomach something like a few billion years for the age of the Earth. A good article on the age-of-the-Earth debate is in Scientific American August 1989 pages 90 to 96. Eventually, physicists had to change their minds about the age of the Sun (and Earth) as radioactive dating indicated a 4.6 billion year age for the solar system and, therefore, the Sun. It was the fact that the Sun could not last long enough being powered by gravitational contraction that motivated the search for nuclear power sources.

To get the positively-charged nuclei to fuse together, their electrical repulsion must be overcome (remember that like charges repel and opposite charges attract---something that rarely happens in human interactions). Once the positively-charged nuclei are close enough together (within several 10-13 centimeters of each other), another fundamental force of nature called the strong nuclear force takes over. It is much more powerful than the electric force and makes the nuclei stick together.

To get those nuclei close enough together requires high temperatures and high densities. At high temperatures the nuclei move fast enough to be driven close enough together for them to fuse. The high densities ensure that there are enough nuclei within in a small volume for the collisions to take place at all. The only place these extreme conditions occur naturally is in the cores of stars.
The temperatures in the cores of stars are above the approximately 8 million K needed to fuse hydrogen nuclei together. The amount of repulsion is larger for nuclei with more positive charge so the fusion of elements with greater positive charge requires greater temperatures and densities than that needed for fusing elements with small positive charge. This is why stars fuse hydrogen nuclei before they fuse other nuclei. For example, the fusion of helium nuclei requires temperatures above 100 million K and heavier nuclei require even higher temperatures. You will see in the next chapter that these ultra-extreme conditions occur in the final stages of a star's life cycle after the main sequence stage.
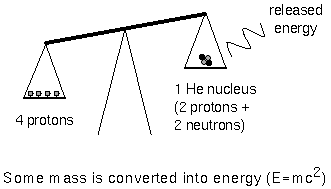
In the cores of main sequence stars, four hydrogen nuclei, each with the mass of one proton, are fused together to form a single helium nucleus (two protons and two neutrons) that has a mass of 3.97 times the mass of one proton. An amount of mass equal to 0.03 times the mass of one proton was given up and converted to energy equal to 0.03 × (mass one proton) × c2. The efficiency of this reaction is about 4/5 of one percent. The Sun could last for about 10 billion years on hydrogen fusion in its core. This is plenty long enough to satisfy the modern geologists.
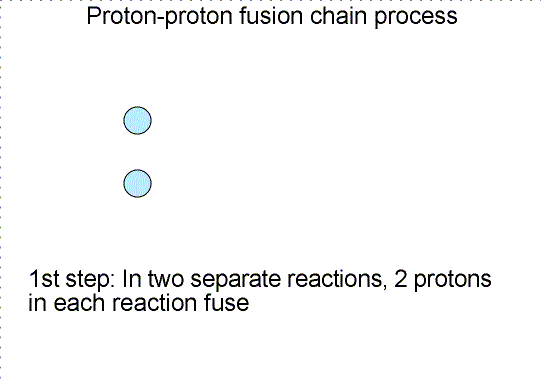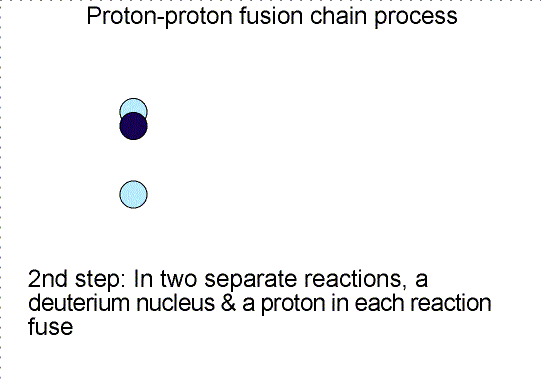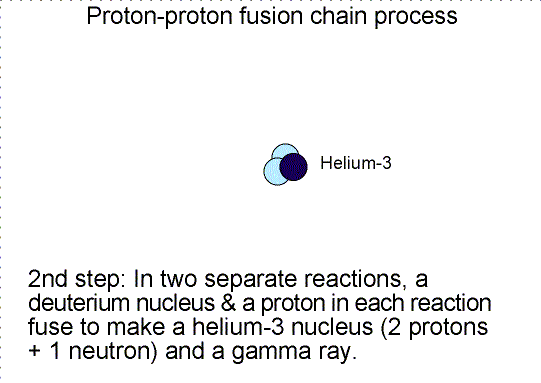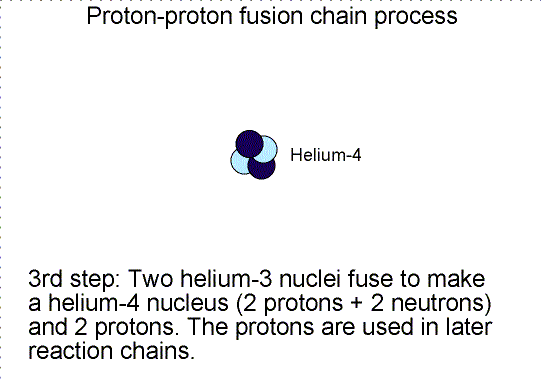
Why does nature use a long complicated chain reaction process to fuse four protons into one helium nucleus? Would it not be much simpler if four protons would collide simultaneously to make one helium nucleus? Simpler, but not very likely is the answer. Getting four objects to collide simultaneously each with high enough energy is very hard to do---the chances of this happening are very, very small (as one from a family of 8 boys I can attest to the difficulty of getting just half of us together for a mini-family reunion!). The chances of this type of collision are too small to power the Sun, so nature has found a cleverer scheme. The chances of two particles colliding and fusing is much higher, so nature slowly builds up the helium nucleus.
Nuclear fusion is something of a holy grail for utility companies because it produces no nasty waste products and has the potential of getting more energy out of it than you put in---free energy! Fusion power would use hydrogen (protons) which we have in great abundance and we could in principle supply enough power for every person on the planet (and billions more) to have access to the same amount of power as the average U.S. resident. Unfortunately, the conditions to get fusion to happen are very extreme by our standards. A major problem is containing the very hot gas for extended periods of time to provide a sustained energy source. We have been able to tap the energy of the fusion process with the Hydrogen bomb, but that is a one shot deal. The Hydrogen bomb still needs an atomic bomb trigger to create the extreme temperatures needed for the fusion process. We have also achieved fusion using many extremely high-energy lasers focused on a capsule of hydrogen smaller than your pinky nail (the National Ignition Facility uses 192 lasers to blast a capsule with a 4 million joule burst of energy in a microsecond). At least you can get the waste product of the Sun's fusion process for free with solar power collectors. The Sun can have a controlled fusion process and not blow up all at once because of the hydrostatic equilibrium ``thermostat''.
Now suppose the nuclear fusion rate speeds up for some reason. Then the following sequence of events would happen: 1) the thermal pressure would increase causing the star to expand; 2) the star would expand to a new point where gravity would balance the thermal pressure; 3) but the expansion would lower the temperature in the core---the nuclear fusion rate would slow down; 4) the thermal pressure would then drop and the star would shrink; 5) the temperature would rise again and the nuclear fusion rate would increase. Stability would be re-established between the nuclear reaction rates and the gravity compression.
A similar type of scheme would occur if the nuclear fusion rate were to slow down for some reason. The fusion rate stays approximately constant for stars that are fusing hydrogen to make helium + energy in the core. Once the hydrogen fuel in the core has been used up, hydrostatic equilibrium can no longer stabilize the star. What happens next will have to wait until I talk about stellar evolution.
![]() Go back to previous section --
Go back to previous section --
![]() Go to next section
Go to next section
last updated: June 19, 2022